Prof. Engel’s Marvelously Improbable Machines

When the path from a simple question to a simple answer leads you through swamps of computation, you can accept that some amount of tromping through swamps is unavoidable in math and in life, or you can think harder and try to find a different route. This is a story of someone who thought harder.

His name is Arthur Engel. Back in the 1970s this German mathematician was in Illinois, teaching probability theory and other topics to middle-school and high-school students. He taught kids in grades 7 and up how to answer questions like “If you roll a fair die, how long on average should you expect to wait until the die shows a three?” The questions are simple, and the answers also tend to be simple: whole numbers, or fractions with fairly small numerators and denominators. You can solve these problems using fraction arithmetic (in the simpler cases) or small systems of linear equations (for more complicated problems), and those are the methods that Engel taught his students up through the end of 1973.

But in 1974 Engel found himself teaching a classroom of struggling 4th grade math students. Despite the students’ difficulties with standard topics like adding and multiplying fractions, he wanted to teach them probability. But how could he do it? Sure, the students could approach probability questions about spinners and dice and coins experimentally, by doing classroom experiments and coming up with empirical estimates, but if they couldn’t follow up on their experiments by computing exact answers and comparing theory with experiment, wouldn’t the students be missing a key part of the learning experience?

And how could the students reliably compute exact answers when standard methods required competency in the very operations (adding and multiplying fractions) that the students were struggling with?

Engel got around the impasse by teaching the fourth graders how to build and operate devices that would efficiently compute exact answers to probability problems. And these devices were made up of nothing more complicated than pieces of paper, pencil marks, and small objects (such as beads or buttons) that could be slid around on the marked-up paper.

AN EASY PROBLEM

We’ll first consider the question “If you toss a fair coin three times, what’s the probability that you get heads twice and tails once (in no particular order)?” We make a diagram that shows, after zero, one, two, or three coin tosses, all the different possibilities for how many heads and how many tails we’ve seen so far.

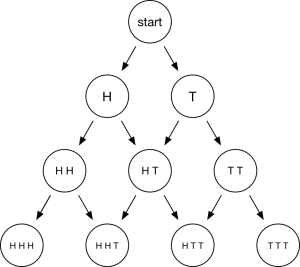For instance, at the bottom of the diagram, the second node is marked HHT, which here means two heads and a tail in no particular order. We also have arrows that lead from a node in any row (other than the bottom row) to two nodes in the next row, corresponding to the fact that at each stage in the coin-tossing process, there are two equally likely possibilities for what happens next, depending on whether the new toss comes up heads or tails. The process of tossing a coin three times can be shadowed by the process of sliding a token down the diagram, starting from the top “start” node and moving progressively down the diagram, sliding the token left when the coin shows heads and sliding the token right when the coin shows tails. The path of the token becomes the primary object of study rather than the sequence of coin flips; we call the path a random walk. The rule for random walking is, when the token is at a node with outgoing arrows, we choose an arrow at random and slide the token along it.

To analyze the behavior of a random walk, we can work our way from top to bottom, successively assigning a number to each node and each arrow, where the number assigned to a node shows the probability that our randomly walking token will visit that node, and the number assigned to an arrow shows the probability that our randomly walking token will slide along that arrow. The probability assigned to the top node (marked “start”) is 1, since the token is certain to visit that node. If we’ve computed the probability p assigned to a node, the two outgoing arrows should each be assigned the value p times 1/2, or p/2. If we’ve computed the probabilities p and q assigned to two arrows that point to the same node at the next level, that new node should be assigned the value p + q.

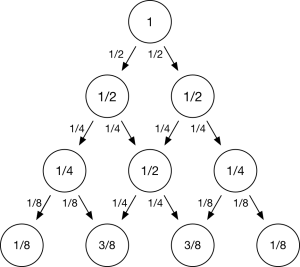If we follow this procedure, we find that the four nodes at the bottom get assigned the values 1/8, 3/8, 3/8, and 1/8. This tells us that the respective probabilities of seeing all heads, two heads and one tail, one head and two tails, and all tails, are 1/8, 3/8, 3/8, and 1/8.

But there’s a way that avoids using fractions until the very end. Engel realized that, properly deployed, the diagram can be a kind of computer. We’ll use small objects call “chips” that can be slid around on a piece of paper and won’t roll away from where they’re put. Suppose we put 8 chips on the node at the top of the diagram (we’ll see shortly where the number 8 comes from). The middle-school rules for assigning fractions to the nodes and arrows correspond to rules for moving the chips. When there are k chips at a node, we equitably move k/2 of them to the left and k/2 of them to the right. We call this chip-firing. 8 chips in the top row becomes 4+4 chips in the next row, which become 2+4+2 chips in the next row, which become 1+3+3+1 chips in the final row. The fourth grader can count the chips in the second node in the last row (there are 3), count all the chips in the last row (there are 8), and divide 3 by 8 to get the answer 3/8.

WHY START WITH EIGHT?

How did we know to put exactly 8 chips into the machine? What if we’d started with a different number of chips? If the number of chips isn’t a multiple of 8, at some point or other it will be impossible to divide the chips at a node equitably between the two outgoing arrows. If, say, we’d started with 7 chips on the top node, we hit a snag right away: we can’t divide the pile of 7 into two equal halves. The best we could do is send three chips to the left and three to the right, but one chip would be stuck on the top node.

Engel’s first big insight was that this stuckness isn’t a fatal flaw for our procedure. We can leave a stuck chip where it is for a while, trusting that sometime later another chip will arrive to free it. In our seven-chip example, if there’s one chip stuck at the top all by itself, adding one more chip (the eighth) will result in two chips being at the top node, and then those two chips can fire.

This leads to a chip-firing algorithm for solving the coin-toss problem that doesn’t involve knowing the magic number eight in advance. We add a chip at the top, fire all possibles nodes, add another chip at the top, fire all possible nodes, etc., until no chips are stuck, that is, until there are no chips in the top three rows. This happens after eight chips have been added, but we didn’t need to know in advance how many chips we were going to add; we just kept going until, magically, the first three rows of the board got cleared out.

I was hoping to include a video of the process I just described, but I didn’t have time to make one. I did however make a video of a related process a couple of years ago, when I was writing about the Pólya urn model. In the urn model, some nodes have 2 outgoing arrows, some have 3, and some have 4, but the ruling principle at each node the same: the randomly walking token has an equal chance of following any of the arrows emanating from the node it’s currently at, and correspondingly, when we fire chips sitting at a node, we divide them equitably among the arrows emanating from the node.

In both the coin-toss model and the urn model, there’s a “magic number” of chips to feed into the start node if we want to end up with all the chips at boundary nodes (nodes with no outgoing arrows); for the coin-toss model the magic number is 8, while for the urn model it was 12. I made two videos about the urn model: in the first video, we know ahead of time that the magic number is 12 (so we load 12 chips at the start node and all divisions work out evenly), while in the second video, we find out that the magic number is 12 by playing Engel’s game (loading chips in one at a time, until adding the 12th chip clears out the top levels of the board).

Henri Picciotto independently reinvented chip firing for problems like this, but he came up with a different way of dealing with the stuckness issue: see Endnote #3.

There’s a potential pedagogical problem with this way of simulating the coin-toss model and the urn model, and that’s the risk that some students will mistake the procedure for an honest simulation. If we were to do eight experiments in which we toss a fair coin three times, we might expect on average that four of the experiments will have the coin show heads on the first toss, but that’s only the average case, and in fact, the chance that our eight experiments will split up in this equitable fashion is only about 27%. Engel’s procedure is not a true random simulation, but a distinctly nonrandom-looking average-case simulation. We call it a quasirandom simulation. (Pseudorandom simulations are as random as we know how to make them, while quasirandom simulations are only as random as they have to be, which in many cases means not random at all!)

Real-world randomness is, as Robert Abelson aptly put it, “lumpy”. Quasirandom simulation smoothes out the lumps, which is good if you’re interested in average-case behavior but bad if you’re interested in typical behavior. The distinction between average and typical is made plain by the old joke that the average person has one ovary and one testicle.

A HARDER PROBLEM

For both the coin-toss process and the urn process, our experiments had a fixed duration. What about random processes that can in principle last any finite number of steps? For instance, let’s take a look at Bruce Torrence’s “Who keeps the money you found on the floor?” puzzle, which was the weekly Riddler puzzle on the FiveThirtyEight website about a year ago. I’ll skip over Torrence’s fanciful story-presentation of the problem and phrase it as a random walk problem. We have a diagram with ten nodes, five on the inside and five on the outside, arranged like this:

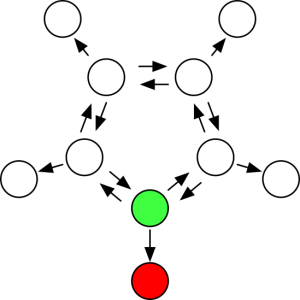Each of the five inside nodes has three outgoing arrows, so when the randomly-walking token moves from an inside node, it has an equal chance (1/3) of following each of the three outgoing arrows, two of which lead to inside nodes (also called interior nodes) and one of which leads to an outside node (also called boundary nodes). Boundary nodes have no outgoing arrows; when the token arrives at such a node, it stays there forever. One of the interior nodes is colored green and an adjoining boundary node is colored red. We want to know, what is the chance that a randomly-walking token that starts at the green node (which we will also call the start node) will end up at the red node?

One thing that makes the problem hard is that there’s no way ahead of time to bound how long the game will take. It’s unlikely that the game will last a million moves (say), but this possibility has a positive chance of happening, so if we pretend it can’t happen we’ll get the wrong answer. At the same time, the probability that the game will go on forever is zero, so sooner or later, the token will arrive at one of the five outer nodes; the question is, which?

You might at first think that each of the five outer nodes has a chance of 1/5 of being the one that the token ends up at, but that can’t be right; after all, the probability that the token ends up at the red node is at least 1/3, since with probability 1/3 the token goes to the red node on its very first move.

We can try to approach Torrence’s problem using chip-firing, as we did with the coin-toss problem and the Pólya-urn problem, beginning from an empty board and adding chips at the start node, doing firing as needed. That is, when we see an interior node with three or more chips on it, we send three chips away from that node, with one chip going to each of the node’s neighbors; we repeat this operation until every interior node has at most two chips on it (that is, until the loading of the chips at the interior nodes is stable). Every time we add a new chip at the green node, we do as many chip-firing operations as are required to restore stability. Then we add another chip at the green node, and do chip-firing to restore stability. And so on, until there are no more chips at any of the interior nodes.

If you try this, you’ll soon see what’s wrong: the interior part of the board never gets cleared out. When an interior node fires, it always fires two of its chips to other interior nodes. So even while many chips find their way to the boundary, there must be some chips in the interior. If our rule for stopping the computation is “wait until the interior nodes are clear”, our computation will go on forever!

ENGEL’S KEY INSIGHT

By playing around with many problems of this kind, Engel hit upon his second key idea. Instead of beginning with an empty loading of the interior nodes (such as we used for the coin-toss process and Pólya-urn process), begin with as full a loading as possible, subject to the constraint that we don’t want any firing to happen at the beginning. In this general setting, an “interior node” is just a node that has one or more outgoing arrows. In the case of the ten-node machine we built for Torrence’s problem, we put two chips at each of the interior nodes (which is the greatest possible number of chips we can put at a node with three outgoing arrows if we don’t want any firing to happen). This is called the maximal stable loading, or the critical loading, of the interior nodes. Our stopping rule is that we end the computation as soon as the critical loading recurs. (See Endnote #4 for more on this issue.) When the critical loading recurs, we can read off the answer by counting the chips that have been absorbed by the various nodes on the boundary. In this case, we get 11 chips absorbed in the outer ring, of which 5 get absorbed at the red node; so the answer to Torrence’s question is 5/11. My Barefoot Math video shows how the computation goes:

This method works for every picture you can draw with nodes and arrows, not just the one that comes from Torrence’s problem. See Endnote #5 for a more technical statement of what Engel actually proved.

Now I can explain the last three words of the title of this essay. “Marvelous” speaks for itself, I hope, though it’s possible that in order to experience an appropriate level of wonder, one needs to acquire some experience in probability theory, solving problems both by the standard method and by using Engel’s chip-firing method. I call the method “improbable” because there’s no randomness in the method of computing the answer (even though the question that’s being answered is about random processes), and more importantly because I think that most probabilists, before encountering this method, would think it highly dubious that such a simple method for solving such a broad array of problems could exist. And “machines”? Well, maybe I should apologize for that word, since a computing device that requires such intensive assistance from its operator (like an abacus) doesn’t usually qualify as a “machine”. Still, when we compare Engel’s method with more traditional paper-and-pencil methods of calculation, we see that an awful lot of the “work” has been outsourced to the diagram and the chips. And we do describe certain sorts of pencil-and-paper operations as “mechanical” (albeit usually in a disparaging way). So I’ll stick with the word “machines”.

Engel called his invention the “probabilistic abacus”, or later, the “stochastic abacus”, but I prefer to say that what he came up with was a technology for designing and operating a whole host of abacuses, each tailored to the problem at hand. An Engel abacus is digital in the sense that, like a general-purpose digital computer, it routes discrete “impulses” (chips) along “wires” (arrows). But it would also be literally accurate to describe each such abacus as being “analog”, in the sense that it is based on an analogy between random walk and quasirandom walk. Indeed, one way to prove that Engel’s abacuses give correct answers is to set up the analogy explicitly, and to show that the “probability-flow” associated with a random walk satisfies the same equations as the flow of chips in the same network. Details appear in Engel’s article “Why does the probabilistic abacus work?”

It’s also possible to create a continuous version of Engel’s devices, in which chips are not indivisible objects but divisible units of some continuous quantity like electric charge (here I ignore the fact that charge is quantized, which makes sense for macroscopic systems like large-scale electrical circuits). There’s a beautiful way in which networks of resistors can serve as continous analog computers for predicting average-case properties of random walk. A lovely book by Doyle and Snell is devoted to this topic.

GAMBLERS AND PIGS

I don’t want to end without giving readers a chance to play with Engel’s ideas on their own, so let me introduce a famous random process and invite readers to study it via Engel’s method. This is the gambler’s ruin problem. Rather than motivate it with the usual oversimplified model of gambling, I’ll present it as a random walk problem on a very simple kind of network:

There are five nodes here: two boundary nodes and three interior nodes. A randomly walking token at an interior node moves to the left with probability 1/2 and moves to the right with probability 1/2. As always, a token that arrives at a boundary node stays there forever. It’s reasonable to suppose (and not too hard to prove) that the token will eventually get absorbed at one boundary node or the other. But which? If the token starts in the middle, then the token is equally likely to end up at the node on the left and the node on the right, but what if the token starts off-center?

I propose a two-part challenge:

1. For each of the three interior nodes, compute the probability that the token will end up at the far right if it starts at the node in question. (You may find it convenient to set up equations expressing each of these unknown probabilities in terms of the other two, and then solve the resulting linear system.)

2. Use Engel’s method to compute these probabilities.

(See Endnote #6 for the answers.)

For extra credit, you may wish to generalize to longer chains with more than five nodes. Can you find a general formula governing the numbers that turn up? And, can you see how thinking about the gambler’s ruin problem via Engel machines led me to come up with the Swine in a Line game?

CONTEXT AND CREDIT

Chip-firing has been rediscovered independently in three different academic communities: mathematics, physics, and computer science. However, its original discovery by Engel is in the field of math education, and I strongly feel that Engel deserves credit for having been the first to slide chips around following these sorts of rules. This isn’t just for Engel’s sake as an individual; it’s also for the sake of the kind of work that Engel did, blending his expertise in mathematics with his experience in the classroom. We often think of mathematical sophistication as something that leads practitioners to create concepts that can only be understood by experts, but at the highest reaches of mathematical research, there’s a love of clarity that sees the pinnacle of sophistication as being the achievement of hard-won simplicity in settings where before there was only complexity.

Giving proper credit isn’t just a matter of rewarding people for their work; it’s also about encouraging others to engage in work of a similar kind. If we want more mathematicians to engage as deeply with pre-college mathematics as Engel did when he taught probability theory at an elementary school, or to come up with improved ways of solving problems that we already know how to solve in a more complicated way, we should at least give the results of those efforts some acclaim. This is all the more true when, as in Engel’s case, the fruits of the enterprise proved to be prophetic of later developments in other, seemingly unrelated fields of inquiry.

I’ve posted Arthur Engel’s unpublished book on my website, with his permission, at http://mathenchant.org/engel-abacus.pdf. Please note that this is Engel’s intellectual property, made available via a Creative Commons license. You may download this work and share it with others as long as you credit Engel, but you can’t change it in any way or use it commercially. Moreover, you must make it clear to anyone with whom you share the book that it is governed by a Creative Commons license, and that they are bound (recursively) by the same obligation. The password for this file is “I Agree”; by using the password to open the document, you are agreeing to be bound by these terms. In particular, it is forbidden to create an unencrypted version of this file.

I’m also hoping to eventually be able to post the PDFs of Engel’s two articles from the 1970s, but there are intellectual property issues involved, so until Springer gives me a green light, I’ll have to content myself with telling you where to look. (If you have a scholarly reason for wanting to read his articles but don’t have access to a library that carries the journal Educational Studies in Mathematics, contact me and I’ll see what I can do for you. I can’t post the articles on the web for all and sundry, but limited forms of sharing are permitted by Springer.)

Note that where I use the word “node” Engel often uses the word “state”, employing terminology from the theory of Markov chains. I wanted to avoid this extra layer of technicality, so in this article I present all Markov chains as random walks on diagrams, but a full appreciation of Engel’s work requires some familiarity with the theory of Markov chains, such as one can obtain from chapter 11 of Grinstead and Snell’s book.

In September, I’ll ask and answer the question, What does Engel’s kind of abacus have to do with the kind of abacus people have used for centuries? As we’ll see, standard systems for representing and manipulating numbers (such as the binary system and the decimal system) correspond to very special kinds of Engel machines, and by turning the correspondence around we can use random processes as inspiration for novel ways to represent and manipulate numbers.

Thanks to David Aldous, Sandi Gubin, Mike Lawler, Henri Picciotto, Shecky Riemann, and Terry Speed.

Next month: How Do You Write One Hundred in Base 3/2?

ENDNOTES

#1. I wrote above: “if [the students] couldn’t follow up on their experiments by computing exact answers and comparing theory with experiment, wouldn’t the students be missing a key part of the learning experience?” Rereading this, I wonder how serious a problem this actually is. Would it be so bad for students to compare their estimates with “the answer at the back of the book”, trusting the authority of the textbook or of the teacher? If the student doesn’t know why Engel’s algorithm works, how is trusting the algorithm any different from trusting the teacher? Moreover, in experimental science, it’s common for students to do an experiment to measure the speed of sound (say) and then check the result by comparing with the speed of sound as reported by a trusted authority. Do you think that this reliance on authority makes the student lab experience a sham? I don’t! The lab experience reinforces the fact that science is a collective enterprise whose reliability stems in part from consistency checks, just like the one the student does when she compare her estimate of the speed of sound with her classmates’ and her teacher’s.

#2. I wrote: “And how could the students reliably compute exact answers when standard methods required competency in the very operations (adding and multiplying fractions) that the students were struggling with?”

I haven’t asked Engel, but I like to think that, in addition to having the fourth graders estimate probabilities with experiments and then compute the probabilities exactly with Engel machines, he also had them try to compute the answers with fractions. I can imagine that giving students a chance to reconcile inconsistent answers obtained by different methods, by having them carry out the procedures with ever-greater attention to detail, would be a great way to motivate the acquisition of fraction fluency.

#3. A different way to use chips to answer the coin-toss problem is to begin with 1 chip at the start node; then double it and do chip-firing, obtaining the loading “1,1” in the next row; then double that loading and do chip-firing, obtaining “1,2,1” in the next row; and finally double one last time and do chip-firing, obtaining “1,3,3,1” in the last row. There’s no reason to stop the process there. Henri Picciotto independently invented chip-firing in this setting, as a way of teaching kids about Pascal’s triangle. What’s more, he came up with a physical activity in which the kids get to be the nodes! See http://www.mathedpage.org/kinesthetics/pascal.html.

One can do something analogous to Picciotto’s doubling trick with the quasirandom Pólya urn simulation, and with quasirandom simulation of many other models. Every time we encounter a situation in which the number of chips at some node is not divisible by the number of outgoing arrows, multiply the number of chips at every node by some number k, where k is chosen to make the divisibility work out. As long as there are no closed loops of arrows, this will give us an expedited way of clearing out all the interior nodes.

You’ve now seen three different approaches to computing “1,3,3,1”. In one of them, we load 8 chips at the start node; in the second approach, we load 1 chip at the start node, and successively add individual chips at that node; and in the third approach, we also load 1 chip at the start node, but instead of adding more chips there later, we multiply the number of chips at each node by some helpful multiplier k when we have to. As long as we’re using an Engel diagram in which there are no closed loops of arrows, all three approaches will give the right answer. But it’s not obvious that the three approaches all give the same answer, let alone give the right answer! That’s part of the magic of confluence: the phenomenon that, for Engel machines (and other processes of a similar nature), lots of different roads lead to the same place. My goal today isn’t to prove confluence, but to convince you that there’s something nontrivial going on here that’s worth understanding.

#4. Why do we begin with the maximal stable loading?

In fact, many initial loadings of the chips will serve Engel’s purposes. More specifically, suppose we initialize an Engel machine with a particular loading of the interior nodes, and then, after adding some (positive) number of chips at the start node and doing some firings, we find ourselves back at the initial loading of the interior nodes. Then we can use the number of chips at the boundary nodes to answer the question “How likely is it that a randomly-walking token that begins its walk at the start node will get absorbed at this particular boundary node?” All that matters is that the initial loading is recurrent; that is, there’s a way to get back to the initial loading of the interior nodes by adding a positive number of chips and doing some firing. The only reason Engel chose to focus on the critical loading is that it’s guaranteed to recur (as a mathematician named Scheller showed). In cases where the empty loading is recurrent, it’s more intuitive to use the empty loading instead. But the critical loading always works. (To see why the critical loading is recurrent, see the article by Snell.)

#5. Here’s what Engel showed: Let S be the start node of an Engel diagram, and let S‘ be a sink node (a node with no outgoing arrows). Let p be the probability that a random walker started at node S will eventually be absorbed at node S‘. Then p is also the proportion of the chips
that end up at the sink node S‘ during the duty cycle of an Engel machine that begins with, and ends with, the critical loading, being fed chips through source node S. The details of the proof don’t actually depend on the assumption that the device begins and ends with the critical loading; all that is required is that the loading of the interior nodes is the same at the end of the computation as it was at the beginning.

To keep the article short, I’ve focussed on how one uses Engel abacuses to compute absorption probabilities, but they can also compute other things, like the answer to a question I mentioned at the beginning of this essay: “If you roll a fair die, how long on average should you expect to wait until the die shows a three?” I may write about this someday; until then, you’ll have to read Engel’s own writings to find out more details.

#6. Let’s record, in each one of the nodes, the probability that a token that starts there will end up at the far right. For the leftmost node, the probability is 0 (since the leftmost node is a sink), and for the rightmost node, the probability is 1 (since we’ve reached our destination before we’ve taken even a single step), but for the other possible starting states, we need to introduce unknowns:

One way to proceed is by finding algebraic relationships between the three unknowns. One such relationship is q = (1/2)(p) + (1/2)(r), representing the fact that if a token starts in the middle, then when the token takes its first step, 1/2 of the time it moves one step to the left (and from there its chance of getting all the way to the right is p), whereas the other 1/2 of the time the token moves one step to the right (and from there its chance of getting all the way to the right is r). Likewise p = (1/2)(0) + (1/2)(q) and r = (1/2)(q) + (1/2)(1). There are various ways to solve this system of three equations for the three unknowns p, q, and r, but one way I like is to write the equations as p−0 = q−p, q−p = r−q, and r−q = 1−r. Since the four quantities p−0, q−p, r−q, and 1−r are equal, and since they add up to 1 (check!), they must each equal 1/4. So p = 1/4, q = 1/2, and r = 3/4.

If we use Engel’s machine, we get the same answer, just moving chips around.

More generally, consider a gambler’s ruin random walk with n+1 nodes, indexed 0 through n. If the token starts at node k, the probability that the token reaches the rightmost node turns out to be k/n. One way to prove this is to follow the algebraic method I described for the special case n=4, and to show that the n+1 probabilities must form an arithmetic progression, beginning with 0 (aka 0/n) and ending with 1 (aka n/n). There is also an approach that uses chip-firing, taking advantage of the idea of conserved quantities and invariants. Decree that a chip at node k has place-value k (as in Swine-in-a-Line), with k going from 0 to n. Chip-firing moves don’t affect the total place-value of the chips, or if you prefer to think physically, the center of mass of the chips. This lets us prove that over the course of the duty-cycle of Engel’s game, the center of mass of the chips that get added at the source must be the same as the center of mass of the chips that get absorbed at the boundary. From this, one can deduce that for every k chips that get absorbed at the right there are n−k chips that get absorbed at the left. Then dividing the number of chips absorbed at the right by the total number of chips absorbed one gets the desired probability k/n.

REFERENCES

Lynne L. Doty, K. Peter Krog, and Tracey Baldwin McGrail, “Probability and Chip Firing Games”, http://dimacs.rutgers.edu/Publications/Modules/Module04-1/fullmodule.pdf.

Peter G. Doyle and J. Laurie Snell, “Random walks and electric networks”; https://math.dartmouth.edu/~doyle/docs/walks/walks.pdf.

Arthur Engel, “The Stochastic Abacus: An Alternative Approach to Discrete Probability”, unpublished manuscript (2008). Available at http://mathenchant.org/engel-abacus.pdf. See above for information about how to unlock the file, and what you are agreeing to when you open it.

Arthur Engel, “The Probabilistic Abacus”, Educational Studies in Mathematics, Vol. 6, No. 1 (Mar., 1975), pp. 1-22; http://www.jstor.org/stable/3482156.

Arthur Engel, “Why Does the Probabilistic Abacus Work?”, Educational Studies in Mathematics, Vol. 7, No. 1/2 (Jul., 1976), pp. 59-69; http://www.jstor.org/stable/3481812.

Arthur Engel, “Remarks on the History of the Probabilistic Abacus”, unpublished; all I have is an nth-generation photocopy (with the figures missing!), rendered as a PDF. It’s noteworthy that Engel explicitly acknowledges Papy’s pedagogical use of the binary abacus as a source of inspiration. It’s also interesting that the two of them clashed in the way that they did; I have a lot of sympathy for both Engel’s position and Papy’s. If anyone has a better copy of this document, please share it with me! My copy is at http://mathenchant.org/engel-remarks.pdf.

Charles M. Grinstead and J. Laurie Snell, Introduction to Probability; https://math.dartmouth.edu/~prob/prob/prob.pdf .

Namrata Kaushal, Madhu Tiwari and C. L. Parihar, “Chip-Firing game as probability abacus by characterization of ULD lattice,” Asian Journal of Mathematics and Applications, volume 2014, Article ID ama0167; http://scienceasia.asia/index.php/ama/article/download/167/92.

J. Laurie Snell, “The Engel algorithm for absorbing Markov chains,” 1979; https://math.dartmouth.edu/~doyle/docs/engel/engel.pdf.