Impaled on a Fencepost

Customer: “But this receipt proves that I bought the phone less than two weeks ago!”

Manager: “I understand, sir. But you can only get a full refund if you return it within fourteen days, and you’re one day late.”

This surreal exchange isn’t from The Twilight Zone. It took place, with me starring as the hapless Customer, in a perfectly ordinary suburb called Watertown, Massachusetts, and this insidious mixture of social and mathematical ills could visit your town too. The social sickness is a familiar one: big companies like Verizon Wireless can screw you over any way they like, and if they screw over enough people in enough different ways, then the people who got screwed over in any particular way will be too dispersed to find one another and take action. The mathematical malaise? Fencepost error.

Cartoon by Ben Orlin (https://mathwithbaddrawings.com/). Follow him on Twitter @benorlin.

OFF BY ONE

Quick: If I eat one piece of candy every day starting November 20 and ending November 30, how many pieces of candy did I have in my stash to begin with? It’s tempting to subtract 20 from 30 and say that the answer is 10, and that isn’t far off, but it isn’t quite right: the number of days between November 20 and November 30, if both endpoints are counted, is 11, not 10. If you said “10”, you’ve committed a fencepost error.

I used the word “between” just now; it’s a slippery one. If I ask you to think of a number between 1 and 10, you’ll probably consider the numbers 1 and 10 to be allowed options. On the other hand, if I ask you how many letters there are between the first ‘e’ and the last ‘e’ in the word “equivocate” you’re likely to answer 8, not 10. When you see the word “between”, watch out! Fencepost error may be lurking nearby.

As you might guess, fencepost error got its name from the task of building fences. Say you’re putting up a 60-foot fence with posts at each end, and you want posts in the middle spaced 12 feet apart. How many posts should you buy? If you divided 60 by 12 to get 5, and you picked up five posts at the hardware store, you’ll have to go back to get another; you’re one post short of a full fence.

Classicists might prefer the term “temple-column error”, since the earliest recorded instance of the error can be found in the writings of the Roman writer Vitruvius. But it’s likely that the error arose much earlier than Roman times; I’m guessing that fencepost puzzlement goes far back in prehistory, to the first human who wondered why she had five fingers on each hand but only four gaps between those fingers.

Here’s an example you may have seen in a movie or in real life: You’re counting the people in a room, and you forget to count yourself. This is a fun one, because if a friend of yours says “Wait, you forgot to count yourself,” and then she counts you but forgets to count herself, she’ll get the same wrong answer as you.

A different sort of fencepost error besets international travellers. In the U.S., the term “first floor” refers to the ground floor of a building; in most other countries, the term “first floor” refers to the level above the ground floor.

The music theorists of the Middle Ages committed a fencepost error that’s too entrenched to dig up now. Consider the chord made of the notes C, E, and G (a C major triad). If music theory nomenclature for intervals made sense, the distance from C up to E plus the distance from E up to G would equal the distance from C up to G. And that’s true if you measure the intervals by counting upward steps. The problem comes when you describe intervals with what I suppose might be termed “ordinal nomenclature”: going from C to E is called going up by a third (because you count 1,2,3 when you play C,D,E) and going from E to G is called going up by a third for the same reason, but going from C to G is called going up by a fifth (because you count 1,2,3,4,5 as you play C,D,E,F,G).

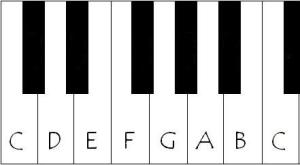The source of the discrepancy should be clear: the E got counted twice when we went C,D,E and then E,F,G, but only got counted once when we went C,D,E,F,G. So in music theory, when you stack a third on top of a third, you get a fifth. We musicians are stuck with nomenclature that essentially makes us say “3+3=5” so many times that we eventually stop noticing we’re saying it. (Of course, saying “a third plus a third is a fifth” is confusing on a different level, since it sounds like “1/3 + 1/3 = 1/5”. But I digress.)

Another place where fencepost errors often creep in is computer code. One source of confusion is the use of different conventions for indexing arrays and lists. In some programming languages the start of a list is called the 1st element, and in others it’s called the 0th. The former convention is more familiar from daily life, but the latter has its charms and turns out to be more convenient in various ways. See Randall Munroe’s take on this controversy.

If you think zero-based numbering is wrong-headed, let’s talk about birthdays. Was the day of your birth your birthday? If so, surely it was your first birthday. But then, the day you turned 1 was your second birthday, and the day you turned 2 was your third birthday, and so on. Most people find this discrepancy untenable, and admit that the day of their birth was their zeroth birthday — except perhaps for people born on February 29, for whom there’s no chance of their birthdays keeping pace with their years of life. (Or people China and elsewhere in East Asia, who start at the age of one year and gain an extra year of age at each New Year’s Day.)

FENCEPOSTS IN MATH

This last example brings us to what should probably be called a fencepost controversy rather than a fencepost error: should we start the counting numbers at 0 or at 1? All mathematicians agree that the term “natural number” includes 1, 2, 3, etc. and excludes −1, −2, −3, etc. (not to mention all the fractions and irrational numbers and other riffraff lurking between consecutive integers), but there’s a lack of unanimity on the question of whether 0 should be included. In some branches of mathematics we start counting from 0; in other branches, we count from 1. I lean toward inclusivity, but in my own writing, I tend to pusillanimously steer clear of the contested term “natural number”, preferring instead to write “nonnegative integer” when I want to include 0 in the club and “positive integer” when I want to exclude it.

There’s also a kind of fencepost fuzziness that we math teachers perpetuate when, speaking informally, we say things like “5 cubed means 5 multiplied by itself three times”. In the expression 5 × 5 × 5, there may be three 5’s, but there are only two multiplications happening! (Defining 5 cubed as “5 multiplied by itself twice” is wrong too, because after the first multiplication, you’re not multiplying 5 by itself anymore — you’re multiplying 25 by 5. But I digress again.)

Students sometimes make the mistake of thinking that the nth term of an arithmetic progression whose first term is a and whose common difference is d is a+nd rather than a+(n−1)d. Likewise, they make the mistake of thinking that the nth term of a geometric progression whose first term is a and whose common ratio is r is arⁿ rather than ar^n-1. These are both cases where it’s natural to think of counting from 0, since the initial term of the arithmetic progression is a=a+0d, while the initial term of the geometric progression is a=ar⁰.

Here are half a dozen puzzles, most of them variants of old chestnuts, that call for careful counting:

1. (my favorite) The ten volumes of an English-language encyclopedia stand on a shelf in the usual way, with volume 1 standing upright on the left, volume 2 to the right of volume 1, and so on. Each volume is two inches thick. Suppose a bookworm starts at the front cover of volume 1 and eats its way in a straight horizontal line through to the back cover of volume 10. How far does the worm travel? (This is puzzle 23 in Martin Gardner’s classic book “Perplexing Puzzles and Tantalizing Teasers”, which my wife and I both loved as children.) See Endnote #1.

2. (a classic suggested by James Davis): A doctor gives a patient 24 pills and instructs her to take two every half hour, starting at noon. At what time does she take the last pill? See Endnote #2.

3. Forty-six children are taking a school trip by bus. Each bus can fit twenty children. How many buses are needed? See Endnote #3.

4. (a classic suggested by Mike Stay): A frog is at the bottom of a well just shy of ten feet deep. He can jump three feet up, but the walls of the well are slippery, so he slides back two feet each time. How many jumps does it take to get out of the well? See Endnote #4.

5. (suggested by Andy Latto): Place a coin with radius 3 on the table, and then place a coin with radius 1 on the table, touching the larger coin. Roll the small coin around the large coin without slipping. How many full turns does the smaller coin make as it goes around the larger, stationary coin once? That is, if the smaller coin is a dime, and Franklin Delano Roosevelt starts with his forehead up and his chin down, how many times does he return to this orientation? Or, what if you roll the big coin around the small coin instead? See Endnote #5.

6. (suggested by Mike Speciner): How many times does the earth rotate around its axis in a year? See Endnote #6.

And, since no list of half a dozen fencepost puzzles would be complete if it didn’t include a seventh puzzle, here’s one more:

7. (based on a suggestion by Henry Baker):

(a) Two swimmers start on opposite ends of a pool. One swims two laps at 2 mph, the other swims three laps at 3.1 mph. How many times does the fast swimmer pass the slow swimmer (going either in the same direction or the opposite direction)?

(b) Same as (a), but now the fast swimmer swims 2.9 mph.

(c) Same as (a) and (b), but now the fast swimmer swims 3 mph.

See Endnote #7.

See also Mike Lawler’s video of his kids tackling a fencepost problem.

IT’S ABOUT TIME

I love Kalid Azad’s explanation of fencepost error at https://betterexplained.com/. It has a great opening paragraph:

“Counting isn’t easy. Suppose your boss wants you to work from 8am to 11am, and mop floors 8 to 11. Simple – it’s one floor per hour, right?”

That sounds good if you’re not thinking clearly. But of course, if you follow that leisurely schedule, you’ll find yourself with one unmopped floor (and one angry boss) at 11am, three hours after you started.

It might seem that we count floors and hours differently, which is weird enough. But Azad isn’t done with his example. Here’s his kicker: he points out that if the boss had instead said “Mop floors 8 to 11 from April 8th to April 11th”, and you’d thought “Great, I can do one floor per day”, you’d have been right. So it seems we also count hours and days differently!

What’s really going on, of course, is as much cognitive-linguistic as it is mathematical. Our minds divide time differently in different contexts: in some settings we focus on stretches of time and ignore the joints between the stretches, and in other settings we focus on discrete events and think of the intervals between events as mere temporal spackle. Even if you and I are thinking of time in the same way, we may use different kinds of language to convey our meaning. And sometimes the language we use is ambiguous.

… which is how I came to find myself arguing with the manager of a Verizon Wireless store a month and a half ago, with a steadily rising sense that I was about to get wrongfully “mathed” out of a hundred and fifty bucks.

SQUARE ONE OR GROUND ZERO?

I’d bought a Verizon Wireless phone at 5pm on September 6, not sure if it was the right starter-phone for my son but confident that if I had buyer’s remorse, I could return it up until 5pm on September 20, exactly 14 days later. I was confident in this belief because the cheerful salesman had told me that Verizon Wireless had a no-questions-asked, all-your-money back policy for items returned within 14 days (not counting the restocking fee, of course).

Alas, I shouldn’t have been so confident. When I brought the phone back to the store on the 20th, the manager (let’s call him Joe, since that’s his real name) explained to me that for purposes of the return policy, the day of purchase counted as day 1, the day after that counted as day 2, and so on. By that reasoning, the day I brought back the phone was day 15, one day outside of the window guaranteed by the return policy.

You can imagine that I tried to use logic with him. I even tried setting up the base case for an argument by mathematical induction: “Would a 1-day return policy mean that I have to return the phone on the same day I purchase it? Even if I buy it at closing time?” But Joe stood his ground. He said he’d been in the cellphone retail business for years, having previously worked at Sprint and T-Mobile, and that all three companies used the same way of measuring time. What’s more, he insisted that if I’d read the hundred-page electronic document that I’d signed when I bought the phone, I would’ve seen a detailed explanation of how the return-policy window worked.

I wasn’t about to give up without a fight. I asked Joe to call Verizon Wireless on his phone and let me talk to them. He said “I can do that, but I’m telling you, I’ve seen lots of people in your position, and the customer service reps at Verizon Wireless aren’t going to tell you anything different from what I’ve told you. I mean, I’d help you if I could, but the computer system won’t let me do a money-back return if it’s outside the return window.”

So, I spoke to a bottom-tier customer service representative at Verizon Wireless (I think it’s called “tier 1” service, but frankly it should be called “tier 0”), and sure enough, he backed up Joe: he said that fourteen days after the date of purchase doesn’t count as within fourteen days for purposes of the return policy. I kind of lost my cool with that guy, but I didn’t actually yell at him, and I did one intelligent thing: while I was on hold waiting to speak to the guy’s supervisor, I called my wife. She suggested a much more convincing style of argument: something not along the lines of “Let n be a positive integer…” (ha ha) but rather along the lines of “If you can’t do things my way, I’ll switch all my lines over to Sprint.” My being able to say this to the supervisor in a calm voice that concealed the rage boiling within, and my having a white male voice and all the societal privilege that goes along with it, did the trick.

The supervisor didn’t issue a refund; his computer (like Joe’s) wouldn’t let him. But he was able to give me a credit applicable toward my Verizon Wireless phone bill, in the exact amount of the purchase price of the phone (minus the restocking charge). So, from my point of view, it was a victory.

In a way, that’s the end of the story. But in another way, maybe the story is just getting started.

WARNING: CONSTRUCTION AHEAD

I started thinking about the people that Joe had referred to — people who had been in the same situation but who, lacking my handy invisible white-male-privilege knapsack and the luxury of spending an hour talking to customer service hadn’t been able to get a refund. Were they ripped off by Verizon Wireless? And, assuming that Joe was right in saying that lots of businesses did business this way, was a lot of this sort of abuse going on? (On the one hand, he had experience with lots of different companies. On the other hand, why did he change jobs so many times? It makes you wonder about the guy; I’m just sayin’.)

I’ll tell you one thing that Joe was wrong about: it turns out that the meaning of “within fourteen days” was not spelled out in the contract that I had signed. So the meaning of “within fourteen days” in the contract is controlled by customary understandings of what the phrase means, as established by courts and regulatory agencies.

In this connection, I learned a fun bit of legal jargon: the phrase “statutory rules of construction”. These are rules that determine how the words of statutes are to be construed. For instance, Massachusetts has a statutory rule of construction that says “The date of issuance of a search warrant is not to be counted in computing the seven day period for the execution of the warrant.” That is, the day of issuance counts as “day zero”, not day one, in the context of the requirement that search warrants must be returned within seven days of issuance. Chalk one up for mathematical common sense!

Statutory rules of construction are usually pretty narrow, as in the search warrant example. And there are differences from state to state. So you’re not going to find a single ruling that says that, for all returned merchandise in the U.S., the day of purchase counts as day zero. Still, based on the limited research that I (or rather my father and sister, both of whom are lawyers) have done, cases going back well over a century by and large support the view that within-a-certain-number-of-days language requires exclusion of the day of the event, in the absence of specific contrary language in the transaction documentation. (If that last sentence sounds impressive, you can thank my father, who wrote the second half of it.)

Here’s a typical example of a statutory rule of construction, from http://www.mass.gov/courts/case-legal-res/rules-of-court/civil-procedure/mrcp6.html: “In computing any period of time prescribed or allowed by these rules, by order of court, or by any applicable statute or rule, the day of the act, event, or default after which the designated period of time begins to run shall not be included.”

Based on other passages like that one, I’ve concluded that Verizon Wireless’s interpretation of the contract that it has its customers sign — an interpretation that Verizon Wireless rigidly enforces in the way it trains its employees and programs its computers — is dubious at best. It’s possible that Verizon Wireless is violating the terms of sale when it denies customers rights accorded to them in the contract.

Also, my father informs me that there’s a kind of meta-rule of construction called contra preferentem, which essentially says that in the situation where a clause in a contract is ambiguous, it should be interpreted in the manner that is least beneficial to the person or organization that drafted the contract. (You can see why this is the right meta-rule to have, since it penalizes sloppy contracts and attempts at deliberate ambiguity.)

HONESTY TIME

Now it’s time for me to admit that legal departments at big corporations are far from alone in the practice of redefining words when it suits them. Lots of people do this. In fact, we mathematicians do it too! But for different reasons.

Consider the question “How many square roots does 0 have?” The commonsense answer is, just one. But mathematicians sometimes have a funny way of counting. In the field of algebraic geometry, we say that the equation x² = 0 has two roots, though if we’re worried that non-mathematicians will call us out on such a provocative piece of nonsense, we’ll say something like “the equation has two roots, counted with multiplicity”, explaining that 0 counts as a double-root of the equation. Having 0 count twice seems artificial the first time you encounter this definition. But it’s an artifice that leads to conceptual economies downstream from the definition.

One way to see where these conceptual economies might come from is to perturb the equation a bit. If c is a positive number close to zero, the equation x² = c has two solutions, while if c is a negative number close to zero, the equation has two solutions (if you’re willing to accept imaginary numbers); so it kind of makes sense that, at least in certain contexts, we’d want to change the way we count so as to make it true that, in some funny sense, there are “two” solutions to x² = 0. If we redefine what it means to counts solutions, then every polynomial equation of degree n has exactly n solutions in the set of complex numbers, when counted “with multiplicity”.

Saying that x¹⁰⁰ = 0 has a hundred solutions, rather than just one, is a lot worse than a mere fencepost error, in terms of its deviation from what initially seems like the sensible way to count solutions to algebra problems.

Such a departure from the way people use language in everyday life might make mathematicians seem like shiftier people than corporate managers. But, unlike the folks at Verizon Wireless, we mathematicians don’t try to hide our definitions (though we aren’t always good at explaining them). For instance, there’s no mystery about double roots; I can tell you right now that a polynomial equation of the form p(x) = 0 is said to have a double root at x=a when the polynomial p(x) can be factored as (x−a)² times another polynomial q(x) that doesn’t have a root at x=a. You didn’t have to wade through a hundred-page document to find this out. Also, when we mathematicians make these seemingly contrived definitions, it’s nearly always because we tried less contorted definitions first, but the downstream consequences of those definitions made us realize that we’d defined things in the “wrong” way.

A more advanced fencepost problem comes from the way mathematicians catalogue spheres. In college math and beyond, the surface of a ball sitting in 3-dimensional space is called a 2-sphere, not a 3-sphere, because its intrinsic geometry — the geometry you’d see if you were living in the space instead of looking at it from outside — is 2-dimensional. Read Evelyn Lamb’s essay on the 1-sphere (aka the circle) for more about this naming convention. Also see her fun essay “How to Confuse a Traveling Mathematician” as an illustration of the way hyperawareness of fencepost error can intrude into a mathematician’s non-mathematical life.

A “DAY ZERO RULE”?

So, what happens next in the story? That’s sort of up to you. We could just leave things there. There are more pressing inequities to address in 2017. The probability of finding enough victims of “off-by-one scams” to constitute a class (in the sense of class action suits) seems minuscule, and the potential rewards scarcely seem worth the effort. (And yes, I know that the word “scams” only applies if there’s an intent to defraud, which has not yet been established. Sue me.)

On the other hand, if mathematician-comedian Matt Parker can get thousands of people in the U.K. to take an interest in the geometric accuracy of roadsigns marking the nearness of a soccer stadium, perhaps someone with more spare time than I have (and substantially more knowledge of the legal system, plus some experience with manipulating the levers of popular opinion) could pick up my banner and march with it, creating a groundswell of support for some sort of legislative action, or maybe just an attention-getting class action suit. According to contra preferentem, the burden of proof would be on Verizon Wireless either to show that it defines “within fourteen days” in its contract (which it doesn’t), OR to convince the court that the term is unambiguous and that its universally accepted meaning accords with the Verizon Wireless interpretation. If Verizon Wireless couldn’t do that, a court would have to side with the frustrated customers seeking redress.

If one wanted to pursue this issue more to raise awareness of mathematics than to prevent big companies from exploiting the ambiguities of contractual language, one might identify the goal of the movement as the proper recognition of the number zero. If Joe is right that there’s a widespread practice among retailers of calling the day of purchase “day one” , maybe this practice can be traced to a mistrust of the number zero. A Day Zero Rule would be a way to confront “zerophobia” head-on and to bring this much-derogated number some of the respect it deserves.

We could also take a more serious point of view, and treat off-by-one scams as a low-tech instance of the ways math is used as an obfuscatory tool of power to intimidate and oppress (as described in Cathy O’Neil’s necessary book “Weapons of Math Destruction“). Then again, I think that those never-read hundred-page waivers that companies force us to sign (thereby dishonestly claiming to have read them) are a bigger problem.

Anyway, I’m hoping something can be done about this sort-of-deliberate sort-of-nondeliberate (“because who can really tell?”) abuse of fencepost error. If we do nothing, then the errorists will have already won.

Next month: The roots of unity.

Thanks to Henry Baker, James Davis, Sandi Gubin, Brian Hayes, Evelyn Lamb, Andy Latto, Mike Lawler, Matt Parker, Henri Picciotto, Sharman Propp, Ted Propp, Shecky Riemann, Leila Schneps, Lynn Siebert, Mike Speciner, Mike Stay, and Glen Whitney.

ENDNOTES

#1. The front cover of volume 1 is not at the left end of the shelf; it’s the part of volume 1 that touches volume 2.  Likewise, the back cover of volume 10 is the part that touches volume 9. So the bookworm only has to bore through 8 books, not 10, traveling a total distance of 16 inches, not 20 inches.

You may have wondered why I specified that the encyclopedia was in English. That’s because if the volumes are in Hebrew, or some other right-to-left language, then the front cover of volume 1 is the leftmost part of the book when it stands on a shelf, not the rightmost. But then, the books wouldn’t have been shelved with volume 1 on the left, would they?

Some of you might say “Well, what if the books are upside down, or the spines are facing inward rather than outward? Ha!” Well, “Ha!” right back at ya: I wrote “… stand on a shelf in the usual way” in the original problem to preempt this sort of quibbling.

#2. The woman will take her last pill at 5:30 pm. (Some people hastily think “24 pills divided by 4 pills per hour equals 6, so she takes the last pill 6 hours later, at 6:00 pm” — though I’m guessing that you didn’t do this, because you figured I wouldn’t include this puzzle if it were as straightforward as that, especially since this essay is about counting errors.)

#3. Many schoolchildren give the answer 2r6 (“two remainder six”), or worse, the answer 2.3. I suspect that, if forced to give a simple whole number as an answer, some children would round to the nearest whole number and give the answer 2. The correct answer is 3, unless you’re a school principal, in which case the correct answer is “Can’t we get some of the parents to chaperone and drive the six extra kids in their own cars? Think of the money the school would save. And it’s not as if those parents have anything better to do with their time.”

#4. Just eight jumps suffice. After the seventh jump, the frog is just shy of three feet from the top of the well, so a single jump will enable him to hop clear of the well.

You may worry that the frog, having jumped up to a place a few inches above the top of the well, but still above the well, will fall back down into the well. But don’t forget, frogs have sticky tongues. Our frog can use his tongue to grab onto the rim of the well and pull himself to safety.

#5. Consider the simpler case where the two coins are the same size (also discussed in my Mathematical Enchantments essay “The Lessons of a Square-Wheeled Trike”). You might expect the moving coin to make one turn, but it actually makes two, as you can verify for yourself if you have two coins of the same denomination.

In this problem, the correct answer is 4 (one more than 3). To see why, look at the points on the two coins that are initially in contact: call them P (on the small coin) and Q (on the large coin), as in the picture below. Assume Q is at “12 o’clock” on the big circle that the smaller coin rolls along (which is also the boundary of the large coin). Some time later, say that points of contact are P* and Q*.  Imagine rolling the small coin back to its starting position, and let P’ be the point that P* ends up at after the rollback.

Since the small coin is rolling around the big coin without slipping, the length of counterclockwise arc PP’ has to be equal to the length of clockwise arc QQ*. But since the radius of the big circle is 3 times that of the radius of the small circle, the angle from P to P’ on the small circle has to be 3 times the angle from Q to Q* on the big circle. (In the figure, these angles are 270 degrees and 90 degrees, respectively.)

When Q* is at 4 o’clock on the big circle, the angle from Q to Q* on the big circle is 120 degrees, so the angle from P to P’ on the small circle must be 3 × 120 = 360 degrees, so that P’ = P. That is, the initial point of contact on the small coin is now touching the 4 o’clock point on the big coin, one-third of the way around. The small coin has made 4/3 of a full turn while its point of contact with the big coin has moved one-third of the way around. If we continue rolling the small coin around the big coin until the point of contact is once again at 12 o’clock, the small coin will have made 4/3+4/3+4/3 = 4 full turns while the big coin will have made none.

What about the variant in which the big coin goes around the small coin? The answer must be the same as in the previous problem, namely 4. To see why, consider the process of rolling the small coin around the big one that we discussed above, but now adopt a moving reference frame in which the small coin stays fixed and doesn’t rotate. In this reference frame, it’s the big coin that rolls around the small one. So now we’ll see the big coin make 4 full turns while the small coin makes none.

#6. An approximately correct answer is 366.25 rotations. A common guess is 365 (since that’s the number of days in a typical year), or 365.25 (since that’s close to the average number of days in a year, allowing for leap years). To see why that’s wrong, consider what would happen if the Earth really made a full turn on its axis in 24 hours. Imagine lying on some comfortable grass, looking up at the Sun at noon on June 1. Now imagine looking up at the sky at noon on December 1, six months later. The Earth has made 183 full turns on its axis, so you’re looking at the exact same point in the sky, but wait — where’s the Sun? It’s on the opposite side of the Earth, where you can’t see it! So now noon is the middle of the night.

What’s going on is that in the course of 24 hours, the Earth actually does slightly more than a full turn around its axis. The surplus is only about 1/365th of a full turn, but add up those slivers of rotation over the course of a year, and you get a whole extra turn.

Puzzle #6 is a lot like puzzle #5, but with more historical significance. Roman priests attempting to implement the Julian calendar, but not fully understanding the relation between days and years, added a leap day every three years instead of every four.

#7. I like to think about this puzzle pictorially. Here’s the picture for part (a):

The width of the picture is 4 pool lengths, and the height of the picture is 6 pool lengths. We represent the progress of the two swimmers by a moving point whose x-coordinate is the distance the slow swimmer has traveled and whose y-coordinate is the distance the fast swimmer has traveled; the thick red line shows the trajectory of the moving point.  The thin black lines mark places where the two swimmers are at the same position in the pool relative to the two ends. A point where the thick red line crosses one of the thin black lines corresponds to an instant when the fast swimmer is passing the slow swimmer. Since there are six such points, there are six such such instants. Two occur quite close together: first the faster swimmer overtakes the slow swimmer (a same-direction pass), then the faster swimmer bounces off the wall, and then the faster swimmer passes the slow swimmer (an opposite-direction pass).

The picture for part (b) is similar:

As before, it’s a little hard to see since some of the points are close together, but we again have six points. This time the two points that are close together correspond to an opposite-direction pass followed by a same-direction pass. Despite the slightly different sequence of events, it’s clear why we get the same answer: in both situations the red path has to cross over one positive-slope (southwest-to-northeast) line and five negative-slope (northwest-to-southeast) lines, for a total of 1+5=6 crossings.

So it stands to reason that the answer for part (c) would also be 6, right? But check the picture:

There are only 5 intersection points, so the correct answer is 5 — although actually, some would say that the real answer here is 4, since the point in the middle corresponds to a moment at which both swimmers simultaneously touch the same end of the pool, which isn’t what we ordinarily would refer to as one swimmer “passing” another.

What’s going on? It’s still true that the red path has to cross over 1 positive-slope line and 5 negative-slope lines, but there aren’t 6 crossings, because one of those 5 negative-slope crossings doubles as the positive-slope crossing.

Here’s a practical way of thinking about it. Even if it looks like the two swimmers touch the wall at the same exact instant, how can we be sure of it? It takes a lot of chutzpah to say that the two events are simultaneous. So, modesty about our measurement process would dictate that we allow those two moments of contact to be different. And if they are, then there’ll be 6 instants when the fast swimmer passes the slow one.

Here’s a fancier way of saying the same thing. A topologist would dismiss the situation described in problem (c) as “non-generic”, arguing that a slight perturbation of the red path causes a sixth crossing to spring into existence. This should remind you of what I wrote earlier about double roots. You might say that, when the fast swimmer and the slow swimmer touch the same wall at the same time, what occurs is an “crossing of multiplicity 2”! Well, you might not say it, but a topologist would.

#8. Brian Hayes makes the clever suggestion that cellphone stores and other brick-and-mortar merchants should define the grace period as “one fortnight”. Most of these stores are only open during the day, and etymologically a fortnight is “14 nights”, so this would make it clear that we are counting not days but the spans between days. (Though I don’t know if Joe and his bosses would accept an etymological argument any more readily than a mathematical one.)

#9. Brian also reminds me of the way our numbering-systems can foster errors. On what day did the current century begin: January 1, 2000, or January 1, 2001? Otherwise reasonable people have strong opinions about this. Likewise, one might consider the fact that the jump-discontinuity between 12:59 and 01:00 on our digital clocks doesn’t occur when we move from one day into the next, but rather an hour later.

#10. I’ll let Lily Tomlin’s character Ernestine have the last word. “We don’t care. We don’t have to. We’re the phone company.”

REFERENCES

Kalid Azad, “Learning How to Count (Avoiding The Fencepost Problem)”.

Edsger Wybe Djikstra, “Why numbering should start at zero (EWD 831)”.

Martin Gardner, “Perplexing Puzzles and Tantalizing Teasers”, Dover Books.

Evelyn Lamb, “A Few of My Favorite Spaces: The 1-Dimensional Sphere”, from her Roots of Unity blog at Scientific American, September 30, 2017.

Evelyn Lamb, “How to Confuse a Traveling Mathematician”, from her Roots of Unity blog at Scientific American, May 10, 2016.

Mike Lawler, “‘Fence Post’ Problems”, from his Family Math blog-vlog.

Cathy O’Neil, Weapons of Math Destruction, 2016.

The Wikipedia entry on Off-by-one error.

The Wikipedia entry on Zero-based numbering.