I’m pleased to announce that the greatest holiday in mathematics is almost upon us: the jubilant festival known as THIRDSDAY!
Huh?
Thirdsday is that magical day on which we celebrate the wonder and mystery of the fraction 1/3.
How come I haven’t heard of it before?
Don’t feel bad; I didn’t know about it either until it was discovered a couple of months ago. Or was it invented? Math can be so ambiguous that way.
Please tell me more. (Because I know you’re going to tell me more whether I want you to or not.)
So glad you asked! Thirdsday comes once every seven years or so, whenever January 3rd falls on a Thursday.
I’m guessing that’s because you’re thinking 1/3 means January 3rd, but doesn’t 1/3 mean the 1st of March in most of the world? So, shouldn’t we celebrate it then?
Not at all! Consider: 1/3, being the simplest fraction that’s bigger than 0 but less than 1/2, is the embodiment of the concept of Minority. So what could be more fitting than celebrating the number 1/3 on a day dictated by a calendrical notation that only a minority of the world’s population uses?
Whatever. Anyway, this is sort of like a Pi Day ripoff, right?
We at Thirdsday HQ think that Thirdsday is better than Pi Day for a whole bunch of reasons. For one thing, 1/3 turns up a lot more than π and is much more useful in most people’s daily lives. Also, 1/3 doesn’t snootily insist on having its own special symbol, and its decimal expansion is a lot easier to remember.
Most importantly, Pi Day comes around too often. It seems that you’ve barely finished writing thank-you notes for the presents you got last Pi Day before it’s time to start start doing your Pi Day shopping all over again. Whereas Thirdsday gives you a chance to recover before the next Thirdsday rolls around.
How do I celebrate Thirdsday?
Any way you want! Unlike certain holidays we could mention, there’s no one who’s going to tell you that you’re celebrating “the wrong way”. But when you’re celebrating Thirdsday, don’t do things by halves; do them by thirds! For instance, have two friends come over and share a pizza three ways. Or share a dozen doughnuts three ways, or a six-pack of beer (or root beer if you’re under age), or a big bag of little candies. Whatever you share, try to share fairly, or at least approximately fairly. And try to do the sharing in a fun way!
How am I supposed to make counting lots of little candies fun?
There’s a cool way to divide a pile into three approximately equal smaller piles, using nothing but the ability to split a pile into TWO approximately equal smaller piles, and a bit of patience.
TRISECTION MADE EASY
Math educator (or, as he styles himself, “math guy”) James Tanton has made a video about how to share a pile of candies three ways. Tanton is the MAA’s Mathematician At Large and also the face of Global Math Week, so he does a lot of traveling; if you do a lot of traveling and like James you want to bring a tie in your suitcase, you’ll want to watch the beginning of the video, where he shows you how to fold a tie in perfect thirds so as to wow the airport personnel who find your lost luggage. Everybody else may want to start about three and a half minutes into the video.
Here’s Tanton’s candy-sharing secret: If you’ve got a pile of candies, split it into a smaller pile and a larger pile (don’t worry about the exact sizes).

Now take the larger pile and split it as evenly as you can by eye into two equal halves.

Take one of those halves and combine it with the previously smaller pile.

Keep doing this over and over: take the larger pile, split it in half, and merge one of those halves with the other pile. The more you do this, the closer you get to a two-to-one split of the candy.1
Also see an essay-with-video in which math vlogger Mike Lawler tries out Tanton’s method with his sons.
The same trick underlies a method for taking cube roots on a calculator that doesn’t have anything fancier than addition, subtraction, multiplication, division, and square roots: if you want to take the cube root of a, repeatedly replace the current approximation x by the better approximation sqrt(a/x). For instance, say you want to compute the cube root of 2; if you start with the bad approximation 1.00 and do the replacement process half a dozen times, you get the better approximation 1.26. 2
SNOWFLAKES AND SNOWFAKES
Standup mathematician Matt Parker is on a crusade against needless geometric inaccuracy in daily life. His most visible exertion in this vein is his campaign to fix depictions of soccer balls on roadsigns in the UK, but he also wants to stamp out what he calls “snowfakes”: winter-themed decorations that purport to be snowflakes but have the wrong number of sides, such as 5 or 8.
In nature, snowflakes have 6 sides; this is a macroscopic consequence of the microscopic structure of ice crystals. (“As above, so below; as within, so without.”) Other sorts of crystalline materials have other sorts of symmetries at the atomic level, and these are reflected in the geometry of the crystals that we see, whether as rare as diamonds or as common as table salt. But the geometry of Euclidean space limits what sorts of repeating forms of atomic structure are possible, and this crystallographic restriction limits the symmetries of macroscopic crystalline structures. No matter how long you stand out in the cold, on our planet or another, no regular pentagon or regular octagon will ever land on your mitten.
Yet many winter holiday decorations feature 5-sided and 8-sided snowfakes. So pervasive is this infidelity to the natural order that even as respected a journal as Science once published an advertisement for itself featuring octagonal snowflakes, causing chemist Tom Koop to issue a stirring call to action. (Note to übernerds: Yes, there are things called quasicrystals that exhibit 5-fold or 8-fold symmetry, but you’re not going to convince me that the people making snowfakes are hip to that.)
Parker’s response to the snowflake-illiteracy crisis has been to address the problem at its root: the kindergarten classroom, where all too often innocent children are forced to make 8-sided snowflakes, which all but guarantees that those children will grow up to be the sort of innumerate adults who say things like “Who cares how many sides a snowflake has? What’s the harm of thinking snowflakes have eight sides? Why are you getting so upset about this? Can you please stop shouting?”
The reason kindergarten teachers force kids to fold 8-sided snowflakes, even though it’s not right, is that it’s easy. Fold a straight angle in half, you get a right angle; fold a right angle in half, you get a 45 degree angle; and now you’re ready to get out some scissors and form an eight-sided abomination. What’s harder is trisecting a straight angle to obtain a 60-degree angle. But it’s not that much harder, and Parker’s video shows how it can be done.
Parker’s trisection is based on origami, which turns out to be a more powerful tool than the straightedge and compass of classical Euclidean constructions (as mathematician Zsuzsanna Dancso demonstrates in a nice Numberphile video). With origami methods, you can trisect any angle and construct lots of n-gons not amenable to straightedge-and-compass construction. So, ironically, the very tool that Parker deploys in defense of hexagonal snowflakes could in principle be used against him in the construction of never-before-seen monstrosities like 7-sided snowfakes4.
For other ways to trisect angles, see Martin Gardner’s article “How to trisect an angle”, which appears as Chapter 9 in his book Mathematical Carnival.
IT JUST GOES ON AND ON, MY FRIENDS
No discussion of 1/3 would be complete without a discussion of the way of writing 1/3 that’s never complete, namely, its decimal expansion, 0.333…. This infinite decimal has the remarkable property that if you replace each digit by the number of sharp points it has, you get 0.333… back again!
High school students are often taught to write 0.333… as

(where the overline above the 3 means “repeat this forever”) and to pronounce it as “zero point three bar”, though I have never heard anyone say this since I left high school. (Actually, when I was watching episode seven of season seven of “Buffy the Vampire Slayer” over a decade ago, I heard the nerdy character Jonathan Levinson say “Of course I’m scared. Last time we were here, thirty-three point three-bar percent of us were flayed alive.” But that’s the exception that proves the rule.)
Mathematical writer and self-proclaimed bad drawer Ben Orlin rightly points out that 0.333… is a newcomer to the lore of one-third, since the fraction goes back thousands of years while the decimal goes back mere centuries. He complains about students who prefer the interloping decimal to the tradition-hallowed and intuitively clearer fraction. See Ben’s graphic essay
(Okay, I added the exclamation mark, but it seemed called for.)
Many students have trouble swallowing the equation 0.333… = 1/3, since they think it means “If you add up enough terms of the sum 3/10 + 3/100 + 3/1000 + … you’ll actually reach 1/3”.5 This misunderstanding of the limit concept often goes hand in hand with the belief that the limit of the sequence .3, .33, .333, … is not 1/3 but something infinitesimally smaller. In this regard, I much prefer the infinite sequence 1/4, 3/8, 5/16, … that we see in the discussion of Tanton’s video in Endnote #1; it approaches the limit 1/3 from both sides, so it’s harder for someone to say that the sequence converges to a limit that’s slightly different from 1/3. (Would that limit be infinitesimally bigger than 1/3 or infinitesimally smaller?)
Those who are jaded by the decimal expansion of 1/3 might profitably look at the binary expansion of 1/3, as Mike Lawler and his sons did. And if you’ve already looked at it, well, you can look at it again.
JOIN IN THE FUN
Even though I just disparaged the decimal expansion of 1/3, it does serve as the basis for a (soon-to-be-) classic activity of Thirdsday: the recitation of the digits of 1/3. The goal of this competitive event, more like a sprint than a marathon, is not to recite as many digits as possible (which could take a long time, and reminds me of one of the more tedious aspects of Pi Day), but rather to recite as many digits as possible in one breath. This constraint guarantees less time spent reciting and listening, and more time spent eating and drinking, increasing everyone’s enjoyment. And memorizing the digits is easy thanks to the simple mnemonic “Bow wow wow wow …”, with the amazing property that the number of letters in the nth word of the mnemonic gives the nth digit in the decimal expansion of 1/3. (Who said dogs can’t do higher math?)
Thirdsday is for everyone. If you’re a college student still on break on January 3, use your freedom from the cares and pressures of college to educate your parents about Thirdsday; explain to them that their buying you pizza and doughnuts and beer is part of your mathematical education. If you’re a high school student, then you’ll already be back in school on January 3, so there’s no excuse for not getting your teachers and fellow students involved in some Thirdsday festivities. And middle schoolers should get involved too. If there’s a middle schooler in your life, please tell her or him that 1/3 is an example of what used to be (and still should be!) called a “vulgar fraction”. I gather that the phrase is still used in England; it ought to be reintroduced in the U.S. I’m sure more middle-schoolers would find fractions interesting if they thought there was something rude about them.
Sounds sort of fun.
Oh, you again! You were so quiet I forgot you were there. Yes indeed, it’s lots of fun for everyone.
I said “sort of”.
Well, 2019 is your one and only chance to get in on Thirdsday on the ground floor. Imagine the nerd-cred you’ll accrue if you can tell people “I was in on Thirdsday when it got started”, while you look pityingly down upon the Poindexter-come-latelies who only heard about it in 2030 or 2036.
I’m thinking I’ll just wait to see if this whole thing takes off and goes anywhere.
Sure, you could do that. I mean, I’m sure that’s what some of Sergei Brin and Larry Page’s friends said back in 1998 about a little startup called Google…
Anyway, I really hope you’ll join us next week, celebrating the vulgar fraction 1/3 and eating lots of doughnuts.
Why doughnuts?
There actually is a mathematical reason. And I’ll tell you all about it next Thirdsday.
Thanks to Sandi Gubin, Evelyn Lamb, Andy Latto, Mike Lawler, Ben Orlin, Matt Parker, Evan Romer, James Tanton, and Glen Whitney.
For more Thirdsday fun, don’t miss Matt Parker’s video Happy Thirdsday: finding a third using only halves, as well as Evelyn Lamb’s How to Celebrate Thirdsday and Ben Orlin’s Thirdsday: the Holiday That’s 33.33…% Better Than Any Other. See also Bill Gasarch’s Today is Thirdsday! Enjoy it while you can! and Zoe Griffith’s Thirdsday-related classroom resource.
Coming up (January 17): The Magic of Nine.
ENDNOTES
#1. We start with a bag of candy whose contents have been arranged in two heaps of unequal size. Say that the smaller heap has size x (in relative terms) and that the larger heap has size 1−x; for instance, if x = 1/4, then a quarter of the candies are in the smaller heap and the remaining three-quarters of the candies are in the larger heap. Tanton tells us to divide the big heap of size 1−x into two smaller heaps, each of size (1−x)/2, and combine one of them with the heap of size x; this gives us a now-small heap of size (1−x)/2 and a now-big heap of size x + (1−x)/2. Tanton claims that if we repeat this process, we get better and better approximations of a two-to-one split. That is, (1−x)/2 (call it x′) is closer to 1/3 than x was, and if we repeat the process, replacing x′ by (1−x′)/2 (call it x′′), we get an even better approximation to 1/3.
In the video, Tanton alternates between small-pile-on-left, big-pile-on-right and big-pile-on-left, small-pile-on-right, but let’s not worry about which pile is where. The point is that if the old small pile had size x, the new small pile will have size (1−x)/2.
It’s going to be inconvenient to write x, x′, x′′, etc. so let’s use subscripts instead: x1, x2, x3, etc.
Let’s see how Tanton’s process works with x1 = 1/4. Then x2 = (1−1/4)/2 = (3/4)/2 = 3/8 and x3 = (1−3/8)/2 = (5/8)/2 = 5/16 and so on. Each time we get a fraction that’s half as far away from 1/3 as the fraction before. In fact, the numbers that we get are partial sums of the infinite series 1/2 − 1/4 + 1/8 − 1/16 + …, which converges to 1/3.
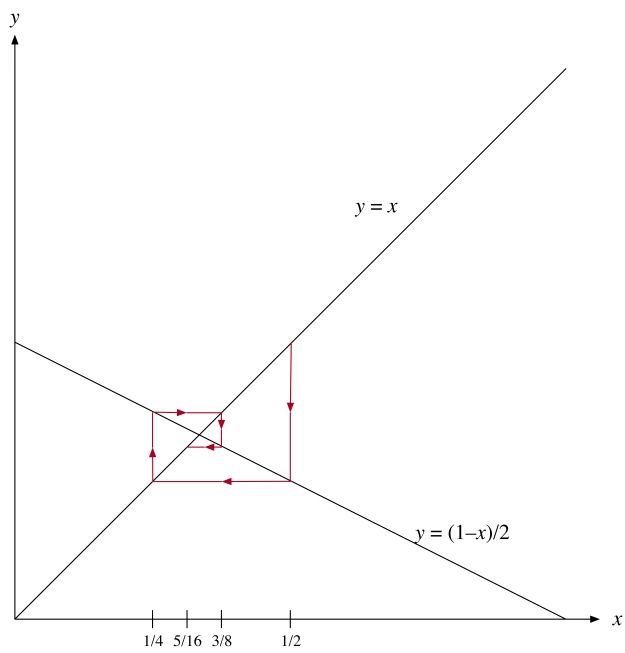
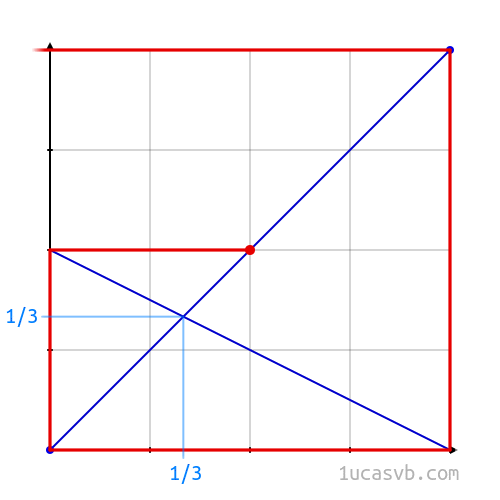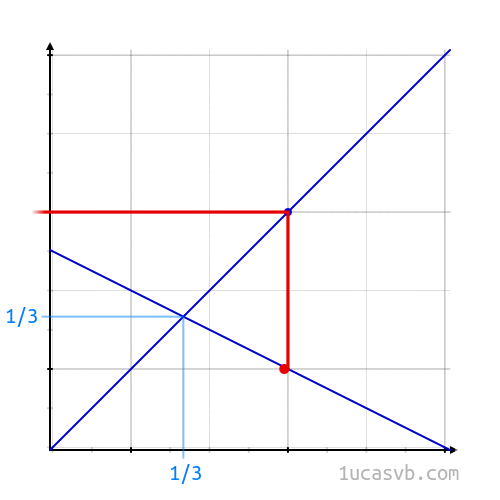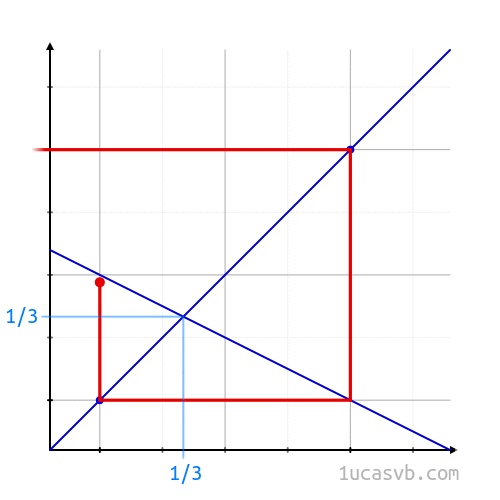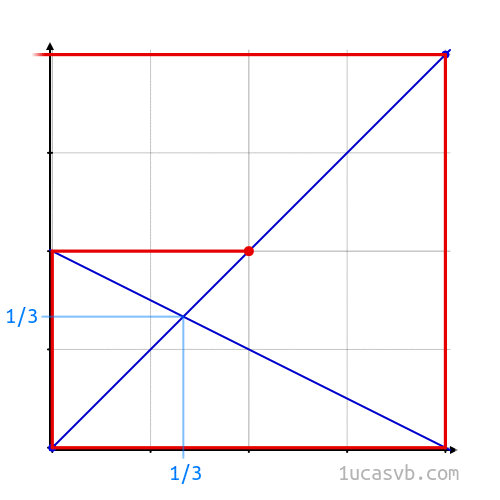
There’s a nice graphical way to understand the process of replacing xn by xn+1. Draw the lines y = x and y = (1−x)/2. Given a point on the line y = x, move down or up (as required) to hit the line y = (1−x)/2, then move left or right (as required) to hit the line y = x again. If we started at the point (xn, xn) on the line y = x, then our vertical step takes us to the point (xn, xn+1) on the line y = (1−x)/2, and our horizontal step takes us to the point (xn+1, xn+1) on the line y = x.
The point (1/3,1/3) where the lines y = x and y = (1−x)/2 meet is what’s called a fixed point of the function that sends x to (1−x)/2. If you let x equal 1/3, (1−x)/2 is equal to 1/3 again. (See Endnote #3 for a caveat about fixed points.)
The diagram (an example of what’s called a cobweb plot) starts the process at the point (1/2,1/2) and ends at the point (5/16,5/16). The video below (created by physics student and educational animator Lucas Vieira) shows what happens if we imagine a dot traveling along such a trajectory forever, moving ever-closer to the point (1/3,1/3), while at the same time we zoom in. Every time the dot makes a complete circuit of the fixed point, it’s closer to the fixed point by a factor of four. So if over the course of the circuit we zoom in by a factor of four, the last frame of our GIF looks exactly like the first frame, so by just repeating the video-loop over and over we reproduce the effect of endlessly zooming in on the fixed point while the moving dot travels an endless square spiral, approaching but never reaching (1/3,1/3).
#2. In a similar way, the cube root of a is the fixed point of the function that sends x to sqrt(a/x). (Check it out: If we square both sides of the equation x = sqrt(a/x) we get the equation x2 = a/x, which simplifies to x3 = a.) Note that if we take the base a logarithms of successive approximations to the cube root of a, the numbers we get are precisely the successive approximations to 1/3 given by Tanton’s process.
There’s another method of computing cube roots using multiplication instead of division: given an estimate for the cube root of a, you can get a better estimate if you multiply your estimate by a and then take the square root twice. That’s because the cube root of a is the fixed point of the function that sends x to sqrt(sqrt(ax)).
#3. There’s an important sense in which the preceding discussion in Endnotes #1 and #2 is incomplete. Consider the operation that sends x to 1−2x; it too has 1/3 as its unique fixed point. But if you apply this operation repeatedly, starting from a number that’s close (but not equal) to 1/3, your approximation gets worse and worse! In fact, this process is Tanton’s process run in reverse. What’s going on is that, for Tanton’s process, the number 1/3 is an attracting fixed point, whereas for the reverse Tanton process, the number 1/3 is a repelling fixed point.
It can be shown that for the two operations mentioned in Endnote #2, the cube root of a is an attracting fixed point. The easiest way to prove this is to take logarithms; then the first of the two processes reduces to Tanton’s process (“Replace x by (1−x)/2″), and the second reduces to a variant of Tanton’s process (“Replace x by (1+x)/4″).
#4. For details on how to fold a regular heptagon, see Robert Geretschläger’s article Folding the regular heptagon. For a description of those values of n for which the regular n-gon is origami-constructible, see Origami constructions by Antonio M. Oller Marcén.
#5. In the original version of this article, I wrote:
Many students who have no trouble swallowing the equation 1/3 = 0.333… gag on the equation 0.333… = 1/3, since they haven’t reified the real number system in their minds and they think of the equals sign procedurally; to them, “1/3 = 0.333…” means “If you try to divide 1 by 3 you get 3’s for as far out as you have the patience to go”, whereas “0.333… = 1/3” means “If you add up enough terms of the sum 3/10 + 3/100 + 3/1000 + … you’ll actually reach 1/3”.
One pre-reader expressed skepticism about this passage, noting that although he’d encountered lots of people who were skeptical “0.333… = 1/3” (and likewise “0.999… = 1”), he’d never met anyone who maintained that equality was asymmetric.
I took out the passage, because it raises issues that I’m not competent to discuss with any authority (and even if I felt competent to opine, my opinions would deserve an essay of their own). But I do feel that confusion about the meaning of the “=” symbol is common, even if the people who suffer from it are unable to articulate it clearly.
My impression is that even though most high school students learn to repeat the mantra “If x equals y, then y equals x“, many of them don’t believe it at a deep level, and their willingness to invoke this principle is context-dependent. Carolyn Kieran’s article “Concepts associated with the equality symbol” (Educational Studies in Mathematics 12 (1981), pp. 317-326) strikes me as still quite relevant to what students think we mean when we write 1/3 = 0.333… or 0.333… = 1/3. Judging from a 2016 mathmisery post, I think that students continue to think of “=” in ways that are subtly different from what teachers intend. But (a) I don’t teach high school and (b) Kieran’s article is nearly forty years old, so if you teach high school and/or you know about more recent literature on this issue, please post in the comments!
#6. For a recent conjecture about the number 1/3, see my recent Mathematical Enchantments essay ChipChip: A new sort of sorting (search for the word “spooky”). If you know of other fun conjectures or facts about 1/3, please post them in the Comments.

Actually, any polyhedron composed of hexagons and pentagons must have exactly 12 pentagons no matter how many hexagons. (Even with zero hexagons, we get the well-known dodecahedron.)
Recalling that V-E+F =2, let H be the number of hexagons, and P be the number of pentagons. Since three edges meet at a vertex and two faces form an edge,
(6H+ 5P)/3 – (6H + 5P)/2 + (H+P) = 2
P=12
W5 (Which Was What We Wanted)
And for years I thought “hexagon” was what a successful Italian exorcist would say.
LikeLiked by 1 person
I wonder if it’s possible to move the pentagons all to the back face of the soccer ball. Then we could manufacture one and send it to Matt with a note saying “See? SOME soccer balls are like that,” just to be annoying.
LikeLike
Pingback: Stance and distance in popular writing about math |
Just read Evelyn Lamb’s followup piece to this where she tosses in the obvious relevance of the Cantor Set (one of my favorite math constructions) to thirder seekers:
https://blogs.scientificamerican.com/roots-of-unity/how-to-celebrate-thirdsday/
A bit of a stretch, but that in turn made me think of the Monty Hall Problem where thirds play a major non-intuitive role (if you don’t switch doors you have 1/3 chance of winning, and if you do you jump to 2/3). And then there is the Sleeping Beauty Paradox where, so far as I know, thirders are stiiiiill battling it out with halfers for the best answer.
LikeLiked by 2 people
Yes indeed. I hope to say more about probabilistic instances of 1/3 on a future Thirdsday.
LikeLike
Pingback: Thirdsday: the Holiday That’s 33.33…% Better Than Any Other – Math with Bad Drawings
Pingback: Today is Thirdsday! Enjoy it while you can! – Site Title
Pingback: Happy Thirdsday! | The Aperiodical
Happy Thirdsday! I actually think that 1/2 and -1 would benefit from special symbols, they occur so often and are awkward to write.
LikeLiked by 1 person
I’m pretty sure some old typewriters had a 1/2 key.
LikeLike
Pingback: Happy Thirdsday! (Thursday 1/3) - Nevin Manimala's Blog
This Thirdsday was specially significant because 2019 is evenly divisible by 3. 2030 is not.
LikeLiked by 1 person
Pingback: Links: 2019-02-01 | Featured Futures
Pingback: The Carnival of Mathematics – Math with Bad Drawings
Pingback: Unreasonable News: Google's Record-Breaking Pi Day Statement - Science and Tech News
Pingback: Chess with the Devil |
Pingback: The Positive Side of Impossible |
Pingback: Breaking Pi |
Pingback: What is a Matrix? |