To err is human; we all make mistakes. But some mistakes have worse consequences than others. According to Greek myth, King Sisyphus of Ephyra made the especially big mistake of cheating Hades, the God of Death. Twice. Hades said “Fool me once, shame on you; fool me twice, you have to roll a huge boulder up a hill only to have it roll back down again, forever and ever.” I like to imagine Sisyphus counting his steps, repeatedly reaching the same top number just before the heart-breaking moment when the boulder returns to the bottom and Sisyphus is back at 1 again. Ironically, this kind of cyclical counting has played a big role in helping us non-mythical people catch our own mistakes in calculations and, more recently, in helping us correct errors in messages we send and receive across vast distances.
We use Sisyphean counting to keep track of time: the hours go from 1 up to 12 and then back to 1 again. When we waltz, we keep track of our movements with “one, two, three, one, two three …” (until we stop consciously counting and just enjoy moving to music in accordance with Leibniz’s observation “Music is the pleasure the human mind experiences from counting without being aware that it is counting”). But the simplest kind of cyclical counting people do (usually unconsciously) goes “one, two, one, two, …” with every odd number in the counting process replaced by “one” and every even number replaced by “two”; Leibniz would probably say it’s part of the pleasure of taking a walk.
UNZIPPING THE INTEGERS
Unzipping the set of counting numbers into two smaller interleaved sets, the odds and the evens, goes back to ancient days. One of the earliest discoveries was that if two numbers are even, then their sum is even. On the other hand, if one of the two numbers is even but the other is odd, then the sum will be odd; and if each of the two numbers a, b is odd, then their sum a + b will be even. We can summarize the situation with a table:
Likewise, if you want to know the odd-versus-even status of the product a × b (also known as the parity of a × b) based on already knowing the parity of a and the parity of b, this second small table will tell you:
These tables point the way toward a kind of number system that differs in an important way from the ones we’ve seen before. Our earlier number systems were governed by an impulse toward expansion; we moved from counting numbers to rational numbers to real numbers to complex numbers and even beyond, always enlarging our store of numbers. Now we go in the other direction, not in the obvious way (by culling some of the numbers) but by lumping: sticking all the even numbers together to create a new entity called Even and sticking all the odd numbers together to create a new entity called Odd. We used what we know about even and odd numbers to create those two operation tables, but once we’ve created the tables, the new mathematical mini-universe we’ve just created becomes independent of the process that gave rise to it. If you want to know the value of (Odd × Odd) + (Even × Even), you don’t need to know what “Odd” and “Even” mean, or even what “+” and “×” mean; you just need to look at the tables.
I’ve said it before, but it’s worth reiterating: this kind of temporary retreat from meaning frees us to consider new kinds of number systems and to get comfortable with them even before we know what they mean or what they’re good for; meanings and applications can come later.
Instead of writing the two elements of our new number system as Odd and Even, let’s choose 1 as our prototypical odd number and 2 as our prototypical even number, so that our new number system consists of just “1” and “2” and the operations of addition and multiplication look like
and
We’ve almost arrived at our first destination for this month, called “mod 2 arithmetic”. To get all the way there, we switch to using 0 and 1 as our prototypes for even and odd numbers.1 Then the tables become
and
These tables may not tell you what mod 2 arithmetic is good for, but they completely tell you what it is.2
A PARITY PUZZLE
A dozen or so people are invited to attend a party at the home of an eccentric billionaire, lured by the prospect of winning a million dollars apiece if they can communally solve a puzzle. (I admit this doesn’t happen very often, but then, neither do wardens of prisons make offers of freedom to those who solve strange puzzles and/or death to those who don’t, as typically happens in the stories surrounding puzzles like this.)
“One hour from now I’m going to put you all in a room and blindfold you and draw a red dot on some people’s foreheads and a blue dot on everyone else’s,” says the billionaire. “Then I’ll remove the blindfolds for a few minutes so that everyone can see everyone else’s forehead. There is to be absolutely no communication of any kind between any of you when the blindfolds are off, or there’ll be no million-dollar windfall for anyone. Then the blindfolds will go back on and I’ll erase all the dots. Finally, I’ll un-blindfold you one at a time and allow each of you to leave the room using whichever of the two exit doors you choose, the one on the left or the one on the right. If all the red-dot people leave through one door and all the blue-dot people leave through the other, then you’ll each get a million dollars. Otherwise, none of you gets anything.”
“There’s one more thing,” he adds. “You can talk among yourselves as much as you like before I bring you into that room, and come up with a strategy for what you’ll do later. But once you’re in that room, there is to be absolutely no communication of any kind. Also, no fair trying to use reflected images of yourself in other people’s eyes, or anything like that, to deduce what color your dot is. It’s not that kind of puzzle. Good luck!”
Perhaps you’ll want to try to solve the puzzle before reading further.
(Perhaps the title of this section is already a bigger hint than you wanted?)
There are two ways to win the game. One way is if all the red-dot people leave through the door on the left and all the blue-dot people leave through the door on the right. The other way is if all the red-dot people leave through the door on the right and all the blue-dot people leave through the door on the left. Don’t try to find a solution to the puzzle in which people are able to deduce the color of their own dot; that is neither necessary nor possible.
One solution is that during the pre-game strategizing session, the guests agree in advance that each guest who sees an odd number of blue dots should go through the left exit while each guest who sees an even number of blue dots should go through the right exit. Why does this work? Suppose that there are n people with blue dots (the guests don’t know n, but “math knows it”). Each of the red-dot people will see n blue dots while each of the blue-dot people will see only n−1 blue dots. One of the two numbers (n−1 and n) is odd and the other one is even, so all of the red-dot people go through one door while all of the blue-dot people go through the other.
If you feel ready for a trickier challenge of the same kind, suppose the billionaire uses three colors of dots (red, blue, and green, say) rather than two and the room has three exit doors. What kind of strategy can the guests agree upon so that all the red-dot guests will go through one door, all the blue-dot guests will go through another door, and all the green-dot guests will go through the third door? I give one such strategy in the next Endnote, though if you are inclined to give up and read my answer, you might want to read the next section of this essay first, as it may provide a clue.3
NOTIONS AND NOTATIONS
In his number-theory masterpiece Disquisitiones Arithmeticae, Carl Friedrich Gauss was dismissive of an excuse put forward by the lesser mathematician Edward Waring. Waring, in his own book Algebraic Meditations, had presented the proposition we now call Wilson’s Theorem (though neither Wilson nor Waring proved it). Waring complained that it was hard to prove such theorems because there was no “notation” for prime numbers (by which I think he meant that there was no formula for the nth prime). Gauss, noting that the mathematicians Lagrange and Euler had both found simple proofs of the theorem, opined that what such problems require are not formulas but ideas – or, as he quipped, “non notationes sed notiones”.
But Gauss knew very well that well-chosen notations can be wonderful tools for thought that guide the mind in the right direction, and one of his most fruitful notational innovations was “a ≡ b (mod n)”, pronounced “a is congruent to b mod n”, meaning that a and b leave the same remainder when divided by n.4 Here “mod” is short for the Latin word “modulo”, and this kind of arithmetic is called mod n arithmetic, or more generically, modular arithmetic. n is referred to as the modulus. For later purposes, I’ll borrow a notation found in some computer languages, and define a%n (pronounced “a mod n“) as the remainder between 0 and n−1 that results from dividing a by n, as per the preceding Endnote.
What’s brilliant about adopting a modified equals-sign for congruence is that congruence has a lot of the same algebraic properties as equality. For instance, if a ≡ a‘ and b ≡ b‘ (here I’m surpressing the “mod n” for brevity and clarity) then a+b≡ a‘+b‘ and a×b ≡ a‘×b‘.5 Having a good notation (in particular, a version of algebraic notation in which = gets replaced by ≡) makes many number-theory propositions easier to prove; your algebraic habits will guide you in the right direction.
What’s also good about “a ≡ b” is what it directs your attention away from, namely, the quotients you get when you divide a or b by n. You might think that the quotients are what matter – after all, in real-life division, we often think of the quotient as the main thing and the remainder as just an annoyance. But in number-theory it’s the other way round. Consider for instance the question of which primes p can be written in the form x2 + y2 where x and y are integers. As Pierre Fermat showed one Christmas day, if p is congruent to 1 or 2 (mod 4) then it can be written as x2 + y2, while if p is congruent to 3 (mod 4) then it cannot. So in particular if you know the last two digits of the prime p – the two least significant digits, from a practical point of view – you know everything about whether p can be written as a sum of two perfect squares (since those last two digits tell you what remainder p gives when divided by 4).
The only thing I can complain about regarding the choice of the symbol “≡” is that you might think that the extra dash in the stack of three dashes is there to provide emphasis – that a ≡ b means “a is really really equal to b” (and indeed, in some other mathematical contexts it has that sort of connotation) – whereas here it means “a is sort of equal to b”. That is, “≡” signifies a weaker condition than “=”, not a stronger one.
You could treat equality as a special case of congruence. Nobody ever writes “a ≡ b (mod 0)”, but if they did, it would mean that a and b differ by a multiple of 0, which is to say that a and b are equal!
Actually, I have one other quibble with the notation “a ≡ b (mod n)”, which is that the “(mod n)” that clarifies the meaning of the “≡” is confusingly separated from the “≡” by the “b”. For this reason, some people write a ≡n b (especially for pedagogical purposes) to make it clearer that the relationship between the numbers a and b that’s being asserted is congruence-modulo-n.
The mathematical term “modulo” has seeped out of math-speak into the nerdier precincts of the English language, with the meaning “ignoring”, “neglecting”, “barring”, or “setting aside”, as in “Modulo the weather, I’ll be there” or “Modulo drying them off, I’ve finished doing the dishes.” We mathematicians sometimes carry the jargon a bit farther and say that mod n arithmetic is the arithmetic you get if you start with integer arithmetic and then “mod out by n”, but I’ve never heard a non-mathematician use “mod out” this way.
FINITE ARITHMETICS
We’ve seen how mod 2 arithmetic works, but if writing 1 + 1 = 0 makes you nervous, you can write 1 + 1 ≡2 0 instead. Or you could define a new operation +2 by the rules 0 +2 0 = 0 = 1 +2 1 and 0 +2 1 = 1 = 1 +2 0 and call it “addition mod 2”.
More generally, we can define a +n b as the remainder you get when you divide a+b by n; that is, we define a +n b as (a+b)%n (keeping in mind what I wrote in an earlier footnote about the meaning of “%”). Likewise, we can define a ×n b as (a×b)%n. This gives us a finite arithmetic with n elements that we write as 0, 1, 2, . . . , n−1. Some people exclude integers outside this range from mod n arithmetic; I prefer to be inclusive, as long as everyone knows that when you’re doing mod n arithmetic, n is just another name for 0, −1 is just another name for n−1, and so on.
Modular arithmetic is also sometimes called clock arithmetic. You picture it on a circle, with points on the circumference that make n equal angles: from 0 to 1, from 1 to 2, and so on, up to the angle from n−1 back to n (which is another name for 0), as shown above for n=12. You might view this as an Escher-ish variant of the Sisyphus scenario where, instead of the rock escaping Sisyphus’ control and rolling back down to the bottom, Sisyphus keeps going up but encounters the same scenery over and over, never reaching the top because there is no top. Titian, meet Escher; Escher, Titian.
Let’s focus on mod 4 arithetic, given by the tables
and
Subtraction in modular arithmetic is no problem; for instance, 1 minus 2 in mod 4 arithmetic is 3. (Check this using the operation table: x = 3 is the unique solution to the equation x +4 2 = 1. If you doubt it, look at the row of the operation table for +4 and zoom in on the column headed “2”. Do you see a “1” in this column? In which row does the “1” appear?) Division is trickier, though. What’s 1 divided by 2 in mod 4 arithmetic? That is, what x in the range 0,1,2,3 has the property that 2 ×4 x = 1? There’s no such x. On the other hand, what’s 2 divided by 2 in mod 4 arithmetic? There are two solutions to the equation 2 ×4 x = 2, namely 1 and 3.
When n is prime, you can do division in mod n arithmetic as long as you’re not trying to divide by 0; but when n isn’t prime (as we saw for n=4), you can get into trouble when you try to divide by a non-0 number that has a factor in common with n.
AN APPLICATION TO TILING
Here’s an application of mod 4 arithmetic to a tiling puzzle. Can you tile a 6-by-6 square with nine 1-by-4 rectangles with no gaps or overlaps? You’re allowed to rotate those 1-by-4 tiles to be horizontal or vertical. If you try it, you’ll find that it gets harder and harder to place the tiles as you go, until finally, there’s no place to put the last tile. Now, a string of failures doesn’t amount to a proof that a cleverer person than you couldn’t succeed where you failed, but here’s a proof that nobody, no matter how clever, can find such a tiling. Mark the unit squares with the numbers 0, 1, 2, 3 according to the following scheme:
(Here the numbers in each row count up in Sisyphean style, that is, repeatedly adding 1 mod 4, and the same is true in each column.)
No matter how you place a 1-by-4 rectangle, the four numbers it covers will be a 0, a 1, a 2, and a 3, whose sum, 6, is congruent to 2 (mod 4). So if (big if!) there were a way to place the nine tiles so as to cover the 6-by-6 square with no gaps or overlaps, the sum of the thirty-six covered numbers would be 2+2+2+2+2+2+2+2+2 (mod 4), which is 2.
But now, suppose we cover the 6-by-6 square with 2-by-2 squares in the obvious way. Each 2-by-2 square covers four numbers that add up to either 4 or 8, so each 2-by-2 tile covers four numbers that sum to 0 mod 4. Therefore the sum of all thirty-six covered numbers is 0+0+0+0+0+0+0+0+0 (mod 4), which is 0. In this calculation, unlike the preceding calculation, there’s no if; we know we can tile the 6-by-6 square with 2-by-2 squares.
The two tilings (one conjectural, one actual) tell us two contradictory things: that a certain sum is congruent to 2 mod 4 and congruent to 0 mod 4. The only possible resolution is that the tiling with 1-by-4 rectangles that we were looking for simply doesn’t exist.6
The same argument can be applied to any rectangle as long as at least one of its two side-lengths is not divisible by 4. There are infinitely many such rectangles, and mod 4 arithmetic, despite being finite, lets us dispatch all of them in one blow. So rather than futilely struggling to find such tiling, you can desist from your labors, happy in the knowledge that no such tiling exists. And you have Sisyphus to thank for it.
SHADOWS
The best way to view mod n arithmetic is not as a fragment of ordinary arithmetic but as a shadow of it.
Here’s an analogy from coordinate geometry. If you imagine a screen on the x-axis and a light source high above it in the y direction, the shadow that the point (1, 2) casts on the x-axis is at x = 1. Two points that are far from each other in the plane can cast shadows that are very close to each other on the line; for instance, the point (1.1, 99) is far away from the point (1, 2) but the two points’ shadows are quite close together. The mathematical term for what we’re doing is projecting the plane onto the x-axis. In doing this, we inevitably lose information. For instance, the point (1,99) projects to the same point on the x-axis as (1,2); knowing the location of the shadow isn’t the same as knowing the location of the source. Indeed, there are infinitely many points that project to x = 1 on the x-axis – a whole vertical line’s worth of points. When we project the plane onto the x-axis, all the points on that vertical line get lumped together. We ignore the vertical coordinate of each point and attend only to its horizontal coordinate.
This is analogous to the way mod 2 arithmetic ignores most of the information in a number, attending only to the remainder the number leaves when you divide it by 2. The main difference is that when we project the plane onto the line, not only are the lumps all infinite, but there are infinitely many of them (one for each point on the x-axis). In contrast, when we project the set of integers to the set containing 0 and 1, each lump is still infinite but there are only finitely many of them, in fact only two of them.7
But there’s a big difference between the two situations. In the geometric shadow-game, if you project a point in the plane onto the x-axis and onto the y-axis, then the two shadows taken together allow you to figure out which point in the plane was casting the shadow. For instance, if the shadow on the x-axis is at 1 and the shadow on the y-axis is at 2, then the point casting the shadow must be (1, 2). In contrast, if I tell you that I’m thinking of a number that’s congruent to 1 mod 2 and congruent to 2 mod 5,, it could still be any of infinitely many numbers: 7 or 17 or 27 or … (or −3 or −13 or …). Knowing what a secret number is congruent to mod 2 and what it’s congruent to mod 5 only tells you what it’s congruent to mod 10, nothing more.
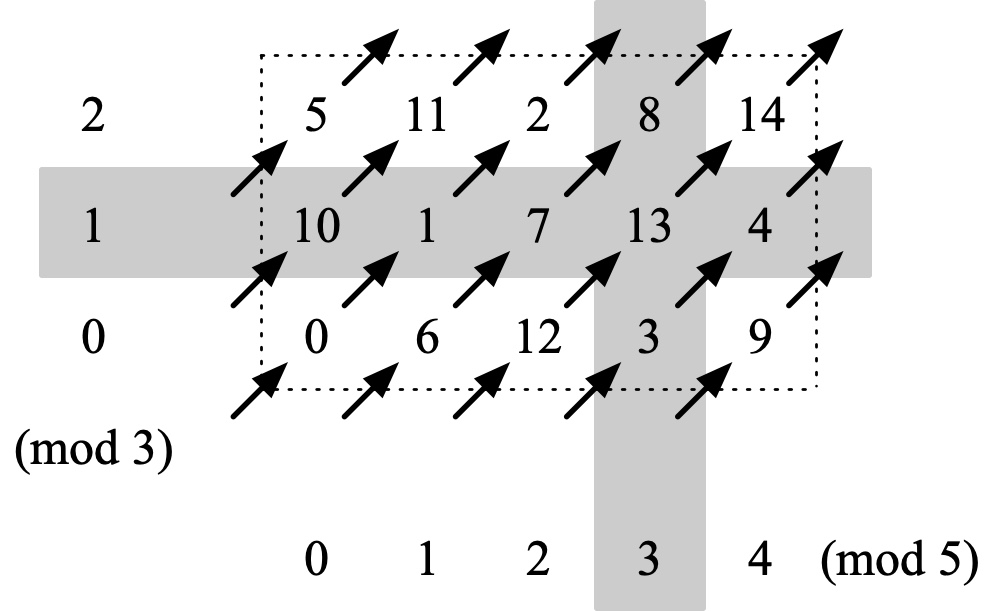
Here’s a diagram illustrating the fact that if you know n%3 and n%5, you can deduce n%15. You can create such a diagram for any two moduli a and b as long as they’re relatively prime (that is, as long as they have no common factor bigger than 1). Start at the bottom left and write 0. Then move one step to the right and one step up and write 1. Keep going, taking diagonal steps. If a step would take you over the top, come back to the bottom; if a step would take you over too far to the right, come back to the left. Eventually you’ll return to where you started and you’ll have filled the entire a-by-b rectangle with numbers (as long as a and b are relatively prime, as 3 and 5 are).
If you’ve got such a diagram, it’s easy to go back and forth between mod-3-and-mod-5 and mod-15. Consider the number 13 for instance. Project 13 onto the horizontal axis and you get 3; project 13 onto the vertical axis and you get 1. This tells us that 13 is congruent to 3 mod 5 and congruent to 1 mod 3. On the other hand, if someone says they’re thinking of a number that’s congruent to 3 mod 5 and congruent to 1 mod 3, just construct the two shaded bands and see where they intersect.
But what if you don’t have a diagram like that in front of you?
The first person who considered such problems was the 3rd century Chinese mathematician Sun Tzu aka Sun Zi (not to be confused with the Chinese general of the same name who had written “The Art of War” several centuries earlier). I’m guessing that before he published his method for solving such problems, he practiced carrying out the method in his head. That is, I imagine that he’d ask you to think of a number between 1 and 105 and to tell him what remainders it left when divided by 3, 5, and 7, and then he would quickly tell you what your number was. (105 arises here because it’s the product of 3, 5, and 7.) His method made use of the three “useful numbers” 70, 21, and 15, artfully chosen so that
If you told Sun Zi that your three remainders (from dividing your secret number by 3, 5, and 7) were 2, 2, and 3 respectively, he would take 2 times 70 plus 2 times 21 plus 2 times 15 (that is, he would multiply your three remainders by his three useful numbers and add those products) and then see what remainder the resulting sum would yield when divided by 105.8 2 × 70 + 2 × 21 + 3 × 15 is 227; subtracting 105 twice gives 17, your secret number.
Sun Zi didn’t explain how he obtained his useful numbers, but it’s not hard to derive them using modular arithmetic.9 Later mathematicians figured out the method behind Sun Zi’s result, and dubbed it the Chinese Remainder Theorem. Personal anecdote: Once back in the 1980s I was eating dim sum in San Francisco with my friend Dan Freed (now a mathematician at the University of Texas at Austin) and two other math-friends, and noticed that most of the plates had six morsels on them, which is great for equitable sharing if there are one, two, three, or six people in one’s party but not good if there are four or five. I asked aloud whether there was some variant of Murphy’s Law that guarantees that when a party of mathematicians goes out for dim sum, the number of morsels on each plate will never be a multiple of the number of people in the party. “Sure there is,” said Dan, not missing a beat. “The Chinese Remainder Theorem.”
I’ll close this section with a puzzle of the Sun Zi variety that you should be able to solve by pure (if tricky) thought, without resorting to Sun Zi’s “useful numbers” approach (or, heaven forbid, trial and error): find a number between 1 and 105 that is congruent to 1 mod 3, 2 mod 5, and 3 mod 7.10
CATCHING YOUR OWN MISTAKES
In the year 950, the Indian mathematician and astronomer Aryabhata II wrote a book called the Maha-Siddhanta, which offered a practical trick for overcoming the human propensity to make mistakes. (I wrote about it in my essay “The Magic of Nine”.) The idea is that you can replace a number n by its digital root, defined as the number you get when you add the digits of n, obtaining a new (smaller) number n′, and then (if n′ is bigger than 9) adding the digits of n′ to obtain an even newer (and even smaller) number n′′, and so on, until you arrive at a single-digit number: the digital root of n. If you added two long-ish numbers a and b and got the total c and you want to make sure you didn’t mess up, Aryabhata II advises you to add the digital roots of a and b (if that sum is bigger than 9, compute its digital root) and compare that with the digital root of c; if they’re not equal, something has gone wrong. What we’re effectively doing is checking whether a + b = c could be true by seeing if the weaker assertion a+b ≡9 c is true. (The main difference between mod 9 arithmetic and the method of digital roots is that mod 9 arithmetic traditionally uses numbers in the range 0,1,…,8, while digital roots use 1,…,9. But it’s just a matter of swapping 0 for 9 or vice versa.)
Likewise, if you’ve multiplied a by b and obtained c as your answer, and you want to check whether you made a mistake, multiply the digital root of a by the digital root of b, take the digital root of that product, and compare that number with the digital root of c. That is, as a way to check whether a × b = c could be true, see if a × b ≡9 c is true.
If you want a finite-arithmetic perspective on why every positive integer is congruent mod 9 to the sum of its decimal digits, recall that the decimal notation “345” for three hundred and forty-five stands for 300 + 40 + 5, or (even more expansively) as 3×10×10 + 4×10 + 5. But in mod 9 arithmetic, 10 is the same as 1, so this expression can be rewritten as 3×1×1 + 4×1 + 5, which simplifies to 3 + 4 + 5.
The Persian thinker Ibn Sina (often called Avicenna in the West), a century after Aryabhata II, passed on what he called the “Hindu method” (much as Westerners dubbed Sun Zi’s theorem the Chinese Remainder Theorem). From there it got picked up by Leonardo of Pisa, who wrote about it in his Liber Abaci. It caught on in Europe, and was widely taught in schools until the 20th century.
It would be hard to convince 21st century schoolchildren of the value of the method (“Why should we learn how to calculate accurately by hand when computers do it so much better?”). But if we look into what goes on inside computers, especially when computers are communicating in networks, we find that there are lots of errors going on all the time, silently being corrected using Sisyphean mathematics, more specifically the arithmetic in which 1 + 1 = 0.
CONQUERING NOISE
Richard Hamming, an applied mathematician at Bell Labs, used mathematics to wage a successful war against noise. Here “noise” is to be understood in a fairly broad sense. Consider, for instance, an overheated vacuum tube in a 1950s-era computer that blows out, so that instead of allowing an electrical signal to pass through it, it blocks the signal. That absence (a kind of silence, electrically speaking) counts as noise, because it messes up the calculation being carried out by the computer that the vacuum tube sits inside. You can replace the busted vacuum tube by a working one and restart the calculation, but wouldn’t it be better if the computer’s processes were more resilient? And the same goes for messages transmitted long distances along wires or through the atmosphere; any number of natural or human phenomena can corrupt the message along the way.
One way living systems achieve resilience is through redundancy; should we take a cue from nature? You could build three computers instead of one, and take their majority vote on any calculation. Or, when sending a digital message, you could transmit the message three times, so that even if one transmission gets garbled, the other two are likely to arrive intact. But this kind of redundancy isn’t very economical. Building three machines to do the work of one is expensive, and transmitting each bit three times reduces the transmission rate (the number of bits per second you’re transmitting) by a factor of three.
Is there some way to reap the benefits of redundancy without paying the awful price of bloat? Hamming found that the answer was yes. Here is the simplest of the schemes he found.
Suppose you want to convey a long string of bits (each a 0 or a 1) over a channel with a low but nonzero amount of noise; maybe every hundredth bit or so will get corrupted (flipped from a 0 to a 1 or vice versa). Divide the string of bits into blocks of length four. For each block of four bits (call those bits a1, a2, a3, and a4), transmit the four message bits a1, a2, a3, and a4 along with three additional bits called check bits, computed as follows:
a5 = a1 +2 a2 +2 a3 , a6 = a1 +2 a2 +2 a4 , and a7 = a1 +2 a3 +2 a4 .
The resulting string of seven bits (four message bits and three check bits) is called a code word, and it is those code words that you transmit across your slightly-noisy data channel. Here are the sixteen allowed code words:
A set of allowed code words is called a code. This code has the property that whenever a1a2a3a4a5a6a7 is a code word and b1b2b3b4b5b6b7 is a code word, then so is c1c2c3c4c5c6c7, where c1 = a1 +2 b1, c2 = a2 +2 b2, etc. That is, the mod 2 sum of any two code words is again a code word. (Why? The check-bit c5 is defined as c1 + c2 + c3, where I’m writing +2as + to make things easier to read, so taking c1 = a1+b1 and c2 = a2+b2 and c3 = a3 +b3 and c4 = a4 +b4, we get c5 = c1 + c2 +c3 = (a1 + b1) + (a2 + b2) + (a3 + b3) = (a1 + a2 + a3) + (b1 + b2 + b3) = a5 +b5, just as we wanted; and the same argument works for c6 and c7.) A code with this property is said to be linear. (We’ll see in a minute why linearity matters.)
We want to see why this code is robust in the presence of single-bit errors. Could it happen that when a bit gets corrupted, the intended code word gets turned into another code word? The answer is no, and there’s a slow way to see it and a quick way. The slow way to see it is to look at each of the 16 × 7 ways to choose a code word w and to choose a location within that code word, and to check that in each case, the result of flipping the bit at that particular location within that particular code word gives a string of seven bits that is not a code word. The quick way to see it is to remember that the code is linear; if there were two code words that differed in just one place, the mod 2 sum of those code words would be a code word containing six 0s and a single 1, and it’s easy to scan the list of code words and see that no code word has a single 1. So there can’t be two code words that differ in just one position. If a single bit gets flipped, the receiver at the other end of the line will know that something is amiss.
In fact, if you scan that list of sixteen code words, you’ll see that each code word (aside from 0000000) has at least three 1s in it, and that’s the secret to the error-correcting capability of this linear code. Could there be a string of seven bits (call it s) that isn’t a code word but is one bit away from the code word w and also one bit away from the code word w′ ? That would be a problem for the decoder, since such an s could have arisen as a garbled version of w (with one bit flipped) or as a garbled version of w′ (with a different bit flipped). But that can’t happen, because then w and w′ would differ in just two locations, which means that the mod 2 sum of w and w′ would have exactly two 1’s in it. And this can’t happen, because the mod 2 sum of the two code words w and w′ is again a code word (remember, this code is linear), and there are no code words containing exactly two 1s.
The upshot is that if a single bit gets flipped, the receiver can do more than determine that an error occurred; the receiver can determine where the error occurred. So the receiver has a way to figure out what block the sender tried to transmit as long as no more than one bit got flipped en route. The receiver first checks to see if the seven received bits form a code word; if so, that’s what the sender sent. If the seven received bits don’t form a code word, then there’s always a unique way to flip a single bit to turn those seven bits into a code word, and that must be the code word the sender transmitted (as long as at most one error occurred).11
Paradoxically, Hamming’s work was so influential that his codes are hardly used at all nowadays. His way of thinking about resilience in digital communication inspired a lot of smart and hard-working people to build on what he’d done and discover even more efficient, even more resilient ways to send data. When your cellphone communicates with the nearest tower, or when NASA communicates with a rover on the Moon or Mars, they’re using the kind of resilience that becomes available when you use an arithmetic in which 1 plus 1 is 0.
I’ll give Hamming the last word, not specifically apropos of this month’s topic, but apropos of the themes of my blog. In his 1980 essay “The Unreasonable Effectiveness of Mathematics” (not to be confused with Eugene Wigner’s 1960 essay with a similar, longer title), Hamming wrote:
“I have tried, with little success, to get some of my friends to understand my amazement that the abstraction of integers for counting is both possible and useful. Is it not remarkable that 6 sheep plus 7 sheep makes 13 sheep; that 6 stones plus 7 stones make 13 stones? Is it not a miracle that the universe is so constructed that such a simple abstraction as a number is possible? To me this is one of the strongest examples of the unreasonable effectiveness of mathematics. Indeed, I find it both strange and unexplainable.”
This essay is a draft of chapter 11 of a book I’m writing, tentatively called “What Can Numbers Be?: The Further, Stranger Adventures of Plus and Times”. If you think this sounds cool and want to help me make the book better, check out http://jamespropp.org/readers.pdf. And as always, feel free to submit comments on this essay at the Mathematical Enchantments WordPress site!
ENDNOTES
#1. Some people put bars over the 0 and the 1, which remind you that you shouldn’t think of these entities as ordinary integers.
#2. I’ve already touched on mod 2 arithmetic in my essay “When 1 + 1 = 0”.
#3. Each guest pretends that the dot on everyone else’s forehead is really a number: red dots are 0’s, blue dots are 1’s, and green dots are 2’s. Each guest computes the sum of all the numbers they “see” on the other guests’ foreheads. If your dot is red, this sum will be n, where n is the total of everybody’s numbers, including your own (which you don’t know but everyone else does); if your dot is blue, this sum will be n−1; and if your dot is green, this sum will be n−2. These three numbers leave different remainders when you divide them by 3. So, if guests leave through the first, second, or third door according to whether the number they compute leaves remainder 0, 1, or 2 when divided by 3, then the conditions of the challenge will be met and each guest will win a million dollars.
#4. It’s important to specify what we mean by “remainder” when the number being dividing by n is negative. You might for instance think that −19 divided by 10 leaves remainder −9, but for Gauss’ purposes and ours it’s 1. When we divide a by the positive integer n, the remainder r is defined as the number between 0 and n−1 (inclusive) with the property that a−r is divisible by n, regardless of whether a is positive or negative.
#5. These properties of congruence are easier to prove if you adopt a different definition of congruence: a ≡ b (mod n) if and only if the difference a−b is divisible by n. This criterion is equivalent to the criterion about remainders, but for many purposes it’s handier to work with.
#6. If this argument seems familiar, you may have seen it last year in my essay “Tricks of the Trade”.
#7. Situations like this are why I don’t like it when people use “infinite” to mean “infinitely many”. In math we frequently need to distinguish between these different manifestations of infinitude. If you talk about a room containing “infinite people”, do you mean that there are infinitely many ordinary-size people or that the people in the room are infinitely tall? If you’re going to use the phrase “infinite lumps” in two different ways, sometimes meaning “lumps of infinite size” and sometimes meaning “infinitely many lumps” according to your whim, do you expect me to do the unpaid cognitive labor of trying to read your mind? If you find this grumpiness tiresome, you probably won’t want to read my essay “In Praise of Pedantry”.
#8. Why does this work? Let’s multiply the columns in the preceding three-by-three table of congruences by 2, 2, and 3 respectively:
Now let’s add the congruences in each row:
We see that 2×70+2×21+3×15 is congruent to 2 mod 3, 2 mod 5, and 3 mod 7, just like your secret number; subtracting 105 a few times gives a number that has the same congruence properties but falls within the target range of 1 to 105.
#9. Start with the numbers 5×7 = 35, 3×7 = 21, and 3×5 = 15. The first of these numbers satisfies 35 ≡5 0 and 35 ≡7 0 but fails to satisfy 35 ≡3 1; instead, it satisfies 35 ≡3 2. So instead of 35, we’ll need a multiple of 35, say 35k, that in addition to satisfying 35k ≡5 0 and 35k ≡7 0 (which work for all k) will satisfy 35k ≡3 1. That is, k must be a multiplicative inverse of 35 in mod 3 arithmetic. Now, 35 corresponds to 2 in mod 3 arithmetic, and the multiplicative inverse of 2 is 2 itself (check: 2 × 2 ≡3 1), so we take k = 2 and get the useful number 35 × 2 = 70. It’s even easier to derive Sun Zi’s other two useful numbers: 21 already satisfies 21 ≡5 1 and 15 already satisfies 15 ≡7 1, so we don’t need to take multiples 21k and 15k to get useful numbers; 21 and 15 themselves will do.
#10. Call this number m. Then 2m is congruent to 2 mod 3, 4 mod 5, and 6 mod 7, so 2m+1 is congruent to 0 mod 3, 0 mod 5, and 0 mod 7. That is, 2m+1 is a multiple of 105. Taking 2m+1=105 gives m=52.
#11. You may (and should) be wondering, why can’t there be a string of seven bits that is neither a code word nor a single-bit corruption of a code word? The answer comes from counting. For each code word w, there are seven ways to corrupt w and one way to leave w alone, resulting in 7 + 1 = 8 words that the receiver will decode as w. There are 16 code words, so this accounts for 8 × 16 = 128 bit strings of length 7. What about the other bit strings of length 7? There aren’t any; the total number of bit strings of length 7 is 27, or 128. This happy coincidence is why the code I’ve described (called the (7,4) Hamming code) is classified as a perfect code.



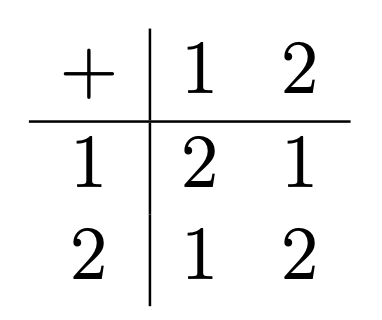
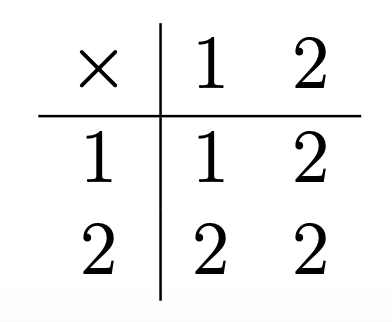
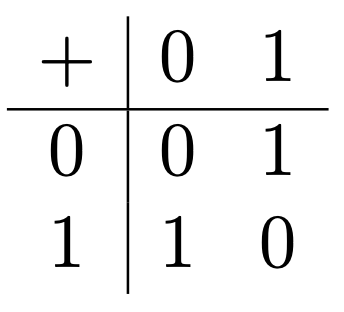
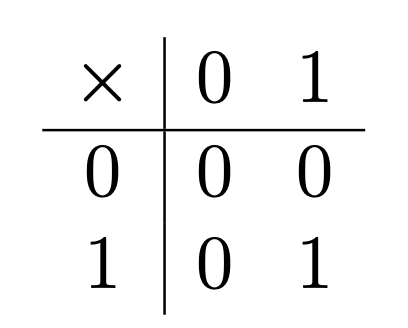









Pingback: 西西弗斯的胜利 - 偏执的码农
Can anyone translate this for me?
LikeLike
Pingback: Marvelous Arithmetics of Distance |
Pingback: Numbers Far Afield |
Pingback: Plus and Times Set Free |