Who Knows Two?

All the work they made them do was rigorous.

— Exodus 1:14

As I write this, it’s April 5, midway through the eight-day festival of Passover. During this holiday, we Jews air our grievances against the ancient Pharaoh who enslaved and oppressed us, and celebrate the feats of strength with which the Almighty delivered us from bondage — wait a minute, I think I’m mixing up Passover with Festivus. In any case, on the first two nights of Passover, Jews tell the story of the Exodus from Egypt before dinner, reading from individual copies of a book called the haggadah (“the telling”), and after dinner they sing a few extra songs, one of which is called “Ekhad Mi-Yodeah?”, or “Who Knows One?” It’s a cumulative song, with each verse containing one more line than the verse before, and in my family the game is to try to get through the increasingly long middle part of each verse without taking a breath. That’s tricky when you get to the last verse, whose English translation is

Who knows thirteen? I know thirteen!
Thirteen are the attributes of God;
Twelve are the tribes of Israel;
Eleven are the stars in Joseph’s dream;
Ten are the commandments;
Nine are the months to childbirth;
Eight are the days to circumcision;
Seven are the days of the week;
Six are the order of the Mishnah;
Five are the books of the Torah;
Four are the mothers of Israel;
Three are the fathers of Israel;
Two are the tablets of the covenant;
One is our God in heaven and earth.

But what does it mean to know a number? Can you really claim an intimate knowledge of the number five if all you know about it is that it’s the number of books in the Torah? Jane Shore, in her poem “Who Knows One” (published in the April 2, 2018 issue of the New Yorker, pp. 70-71), expands on the rabbinic text by giving multiple instances of each number. Five, for instance, are the cents in a nickel, the “wh-?” questions (who-what-where-when-why), and the rivers of the underworld, among other things. Folded into the poem are casual intimate details of a life shared with a lover (perhaps a spouse: “Seven the times the bride circles the groom”). Also scattered through the poem are references to the lover’s infidelity and the eventual end of the relationship. The poem and its title suggest the tragic limits beyond which we can never truly know another person. But we can know something simpler than a person, like a number. Right?

WHAT IS A NUMBER, THAT A MIND MAY KNOW IT?

Shore’s expansive approach to the question “Who knows n?” (for 1 ≤ n ≤ 13) reminds me of the logician Gottlob Frege‘s definition of the number n as the class of all sets that have n elements (or, as he would have put it, all concepts that have n instances). In the spirit of the writer Jorge Luis Borges, inventor of the famous Library of Babel, we might imagine a Gottlob Frege Memorial Library of Natural Numbers, consisting of infinitely many books, one for each nonnegative integer. Every book in the Library must have infinitely many pages in order to accommodate the infinitely many concepts having the specified number of instances.

Leaving aside the sheer impossibility of the human mind ever knowing all the different things that there are five of, Frege’s approach feels incomplete to me. As the poet Shore points out, the number five is prime (or, as she puts it, “indivisible”), yet this fact about the number five is nowhere to be found in the book called “Five” in the Frege Library. For me as a pure mathematician, knowing the number five entails knowing important mathematical facts about the number five — such as “five is prime”, “five is a Fibonacci number”, “five is a Catalan number“, and so on. This is the kind of number-knowledge that interests me. Do I know five in this sense? There are certainly gaps in my own knowledge of individual small numbers like five, but that’s not surprising. A better question is, Are there gaps in the whole of humankind’s knowledge about small numbers like five?

The answer is, Yes! In fact, I know a couple of questions about the number two that are still unresolved by the mathematical community. I won’t dwell on the first question for long, because too many of you already know about it: it’s the twin prime conjecture, which asserts that there are infinitely many pairs of primes that differ by exactly two, the way 5 and 7 do. As a matter of fact there’s a great new book by Vicky Neale about a recent breakthrough that has pushed us closer toward proving the twin prime conjecture.

But what I want to focus on today is a less well-known conjecture asserting that infinitely many primes have 2 as a primitive root. This sounds arcane until you find out its relation to cheating at cards.

THE FARO SHUFFLE

The card game Pharaon seems to have originated in 17th century France (and probably owes its name more to faddish orientalism than to any sort of Egyptian origin). Imported to England as “pharo” and then to the U.S. as “faro”, the game became America’s favorite gambling pastime in the late 19th century. Cheating was rampant, in part because of the ease with which skilled card-mechanics could appear to be randomizing a deck while in fact doing no such thing. The phrase “faro dealer’s shuffle” can be found in an 1894 book on card cheating, and later was shortened to “faro shuffle”. According to Diaconis, Graham, and Kantor, “it is still widely used as a method of cheating at card games such as gin rummy and poker.”

Most people can do an imperfect sort of faro shuffle by splitting a deck into two roughly equal halves and weaving them together in small-ish clumps. This isn’t a great way to randomize a deck, but it isn’t awful; lots of patterns that existed in the deck prior to the shuffling will continue to be present in some form afterwards, but the unpredictable nature of the clumping make it hard for an adversary to predict or exploit those persisting regularities in a reliable way.

The real problem is the perfect faro shuffle. Suppose I place a bunch of cards at the top of a deck, perform three perfect faro shuffles, and invite you to cut the deck before I deal out the cards to the two of us. As we’ll see later, those formerly consecutive cards are now spaced further apart (eight cards apart, to be precise), and maybe I can’t control which of us will get them, but I can be certain that whoever gets one of those cards will get all of them; and you can imagine that this kind of information could be very useful in the course of a game.

I first learned about faro shuffles from the Martin Gardner essays “Chicago Magic Convention” and “Card Shuffles”. It was also from Gardner’s writing that I became acquainted with the great mathematician/statistician/magician Persi Diaconis, who has co-written with Ronald Graham a whole book about the mathematics of magic. If you give Diaconis a deck of 52 cards, he can faro-shuffle it exactly eight times in such a way that, instead of being super-scrambled, the deck is actually restored to its original state!

Why does performing 8 faro shuffles have the same effect as performing 0 faro shuffles, which is to say, performing no shuffles at all? Here’s a simplified analysis of the faro shuffle that uses a deck of 8 cards instead of a deck of 52. Let’s start by labeling the cards A through H, so we can keep track of where they go:

Split the deck into two equal halves and lay them side by side, with the top half of the deck on the left and the bottom half of the deck on the right:

Now merge those two half-decks, riffling together the first card on the left, the first card on the right, the second card on the left, the second card on the right, and so on.

(Magicians call this particular way of merging the two half-decks an out-shuffle; it has the feature that the two outside cards, aka the top card and the bottom card, stay on the outside. Later on I’ll talk about the other way of merging the two half-decks, called an in-shuffle, where the alternation goes right-left-right-left-… instead of left-right-left-right-…)

I claim if you out-shuffle an eight-card deck exactly three times, you’ll get back the original ordering of the cards.

COUNTING CARDS

One helpful way to see what’s going on is to focus on the position of a card before and after the faro out-shuffle, where the top card is in the 0th position, the next card is in the 1st position, the next card is in the 2nd position, and so on. (It might be helpful to think of the card in position i as being the card that has i cards on top of it.)

Here’s a table that shows where the ith card ends up, for i going from 0 to 7:

The cards in positions 0 and 7 stay put, and you can check that for i between 1 and 6, the card that starts in position i ends in position j, where j = 2i for i = 1, 2, or 3 and j = 2i−7 for i = 4, 5, or 6. In all six cases, j is the remainder you get when you divide 2i by 7.

Let’s see what happens when we perform the procedure one time, then a second time, and then a third:

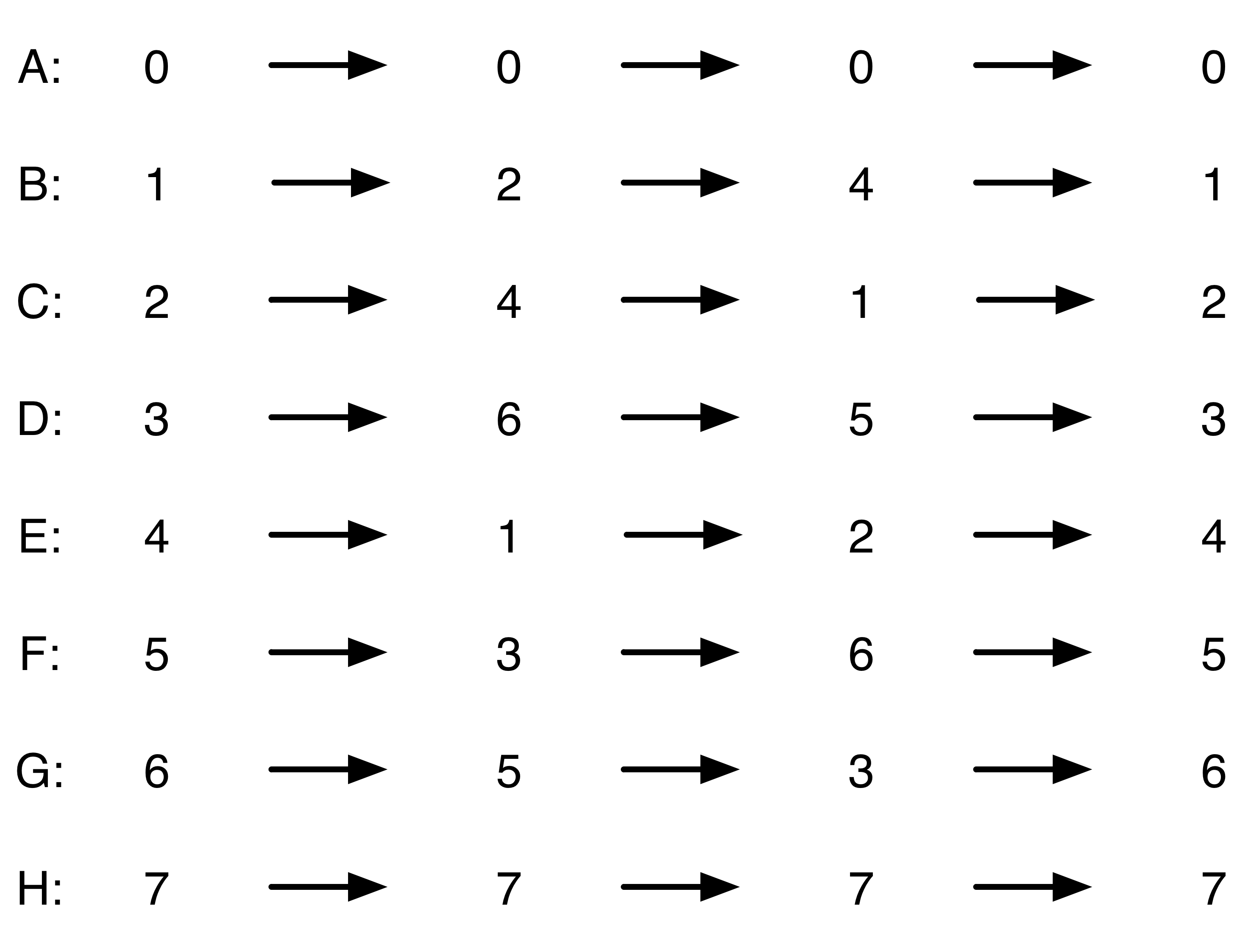
Pick your favorite integer i that’s bigger than 0 and less than 7, and follow the journey of the card that started in position i. You’ll find that after one shuffle, the position of your card is the remainder you get when you divide 2i by 7; after two shuffles, the position of your card is the remainder you get when you divide 4i by 7; and after three shuffles, the position of your card is the remainder you get when you divide 8i by 7, which just so happens to be equal to i itself, so that the card has come back to where it started. (Notice that the number we keep dividing by here, namely 7, is one less than the number of cards in the deck. That’s going to matter in a minute.)

Something similar happens when we repeatedly out-shuffle a larger deck. For instance, take a 52-card deck. The card that starts in position 1 goes to position 2 after one shuffle, then to position 4 , then position 8, then position 16 (hey, the position is doubling every time!), then position 32 (yep, definitely doubling), then position 13 — which seems to break the doubling rule, but wait a moment: were we really expecting the card to go to position 64? There is no position 64 in a deck of 52 cards! But if we divide 64 by 51 (one less than the number of cards in the deck), the remainder is 13.

It can be shown that if you do m faro out-shuffles of a deck with 2n cards (with positions numbered from 0 to 2n−1), then for all i bigger than 0 and less than 2n−1, the card that starts at position i ends up in position j where j is the remainder you get when you divide (2^m)(i) by 2n−1. (See Endnote #5.)

Now we can say why 8 is a magic number when it comes to repeatedly out-shuffling a deck of 52 cards: for every i between 1 and 51, if you divide (2⁸)(i) by 51, you just get i back as the remainder. That’s because 2⁸ is 1 more than a multiple of 51; specifically, 256 equals 5 × 51 plus 1. See Endnote #6 for a more detailed discussion.

But if that’s too abstract for your taste, let’s just go back to following the card that started in position 1, one shuffle at a time. When we last left that card, six shuffles had brought it to position 13.  A seventh shuffle brings it to position 2×13 = 26. An eighth shuffle brings it to position 2×26 = 52, or rather, to position 1 (since 1 is the remainder you get when you divide 52 by 51). So eight shuffles have brought the card back to its original position; and the same is true for every other card in the deck.

THE INS AND OUTS OF SHUFFLING

There’s a close connection between in-shuffling and out-shuffling. When you out-shuffle 2n cards, you’re effectively in-shuffling the 2n−2 inner cards. (Look back at our 8-card deck example, and see the way cards B, C, and D interleave with cards E, F, and G.) Turning this around, when you in-shuffle a deck of 2n cards, it’s just like imagining two invisible cards (one on the top and the other on the bottom) and performing an out-shuffle on the enlarged deck of 2n+2 cards. In particular, an in-shuffle on a standard deck of 52 cards behaves the same way as an out-shuffle on a deck of 54 cards. The number of times you have to in-shuffle a deck of 52 cards before it comes back to its original state is equal to the number of times you have to out-shuffle a deck of 54 cards before it comes back to its original state — and that in turn is equal to the smallest positive integer k for which 2^k is 1 more than a multiple of 53.

The German mathematician Carl Friedrich Gauss was very interested in the problem of determining, for every pair of positive integers a and p having no common factor, the smallest positive integer k for which a^k is 1 more than a multiple of p; he dubbed it the multiplicative order of a modulo p or just “the order of a (mod p)” for short. (If you’re wondering how Gauss got interested in this, see Endnote #7.) We’ve seen that the order of 2 mod 51 is 8. On the other hand, the order of 2 mod 53 is 52. It can be shown that when p is an odd number, the order of 2 (mod p) is at most p−1. So, from the point of view of repeated in-shuffling, a deck of 52 cards has as long a “recurrence-time” as it possibly could.

We can now ask, for what values of the odd number p is the order of 2 modulo p equal to p−1? (These are exactly the odd numbers p for which a deck of size p−1 require a full p−1 in-shuffles before it comes back to its original state; they are also exactly the odd numbers p for which a deck of size p+1 require a full p−1 out-shuffles before it comes back to its original state.) If you do some experiments, or look at the table in Gardner’s essay “Card Shuffles”, you’ll see that the values of p with the property in question are

3, 5, 11, 13, 19, 29, 37, 53, …

Notice anything about these numbers? They’re all prime!

That’s not an accident. It’s not too hard to show that if the order of 2 modulo p is p−1, the odd number p must be prime. But you also noticed that not every prime is on this list.

There’s no simple formula for the order of a (mod p), but we know many things about it. For instance, Euler’s theorem tells us that a^p−1 is 1 more than a multiple of p, so the order of a mod p is at most p−1. In fact, with a bit more work you can show that the order of a mod p must be a divisor of p−1. This fact plays a role in the solution to a recent FiveThirtyEight Riddler puzzle that was submitted by Joseph Converse and brought to my attention by David Merfeld: “Imagine taking a number and moving its last digit to the front. For example, 1234 would become 4123. What is the smallest positive integer such that when you do this, the result is exactly double the original number?” (See Endnote #8 for part of a solution.)

ARTIN’S CONJECTURE

A primitive root mod p (where p is prime) is a number a whose order mod p is p−1. The question “For which primes p is the order of 2 mod p equal to p−1?” is equivalent to the question “For which primes p is 2 a primitive root (mod p)?”

Mathematician Emil Artin played with this question for a bit, and he became convinced in the 1920s that there are infinitely many such primes, but he wasn’t able to prove it. Nobody else has been able to prove it, either.

But here’s something strange. It’s been shown (see Theorem 1 in Murty’s article) that at least one of the numbers 2, 3, 5 is a primitive root modulo infinitely many primes p — but we can’t prove that this is true for any one of the three numbers in particular!

Cartoon by Ben Orlin. Check out https://mathwithbaddrawings.com/.

Does that not seem bizarre to you? Many decades ago, Warren McCulloch asked a two-part question that, in this century, might be phrased as “What is a number, that a mind may know it, and what is a mind, that it may know a number?” The fact that we can write down three propositions (“2 is a primitive root for infinitely many prime moduli”, “3 is …”, “5 is …”) and prove beyond any doubt that at least one of them is true, without getting information about which one is true, even though we suspect all of them are — make me want to ask another question: What is it about minds, numbers, and knowledge that enables the mind’s knowledge of numbers to exhibit such a strange mixture of certainty and ignorance?

You might find this state of affairs less puzzling than I do; after all, life is full of situations analogous to this (such as knowing that one of two children started a fight without knowing which). But what’s going on in such cases is that some action took place out of sight, or some information has been rendered inaccessible by the passage of time. With math, there’s no hidden information, and indeed (if you’re a certain kind of materialist) no place in the world where the information could hide, since math is entirely in our heads to begin with!

Compounding the irony of our ignorance about 2, 3, and 5 is the fact that, even though we haven’t proved that there are infinitely many primes p for which 2 is a primitive root mod p, it appears to be the case that over a third of all primes have this property. Artin conjectured that as you take the cutoff N larger and larger, the proportion of the primes p up to N that have 2 as a primitive root approaches the value

(now called Artin’s constant). This more detailed conjecture is borne out by computer evidence, and if this conjecture is true, it implies the weaker conjecture that the number of such primes is infinite. Yet we still don’t know how to prove that there are infinitely many primes for which 2 is a primitive root.

Even more interesting is the origin of Artin’s constant via nonrigorous probabilistic reasoning. Artin asked “If p is some large prime, what are the chances that 2 will be a primitive root mod p?” Artin used probability theory to get an answer (see page 5 of the article by Moree), but it’s not clear why the answer should be right, since the premises on which probability theory rest do not apply literally to the study of primes; for any particular prime p, either 2 is a primitive root mod p or it isn’t. Yet in this case (and many other cases), probabilistic arguments do a surprisingly good job of giving the right answer (or at least answers that are well-supported by empirical evidence). Eugene Wigner and Richard Hamming wrote of the “surprising effectiveness” of mathematics in the study of nature; hardly less surprising is the effectiveness of probability theory in the study of nonrandom subjects like number theory.

These sorts of mysteries reveal a profound gulf between what we can guess and what we can prove, and show just how far the human species has evolved in its mathematical understanding, which is to say, not very far. We’re like the simple child described in the hagaddah who, confronted with the complexity of Passover rituals, can only say “What is this?” It may not be the right question, but at least we know how to ask a question, which is a start.

THE BIG QUESTIONS

Let’s finish by returning to the questions that puzzled Gottlob Frege (at the start of this article) and Warren McCulloch (a few paragraphs back): What are numbers, and how do we understand them? One answer modern mathematics gives is, in a sense, “Number is as number does.” That is, numbers are things that behave in a particular way when you add, subtract, multiply, and divide them to obtain new numbers from old. This is an essentially relational view of the ontology of numbers: no number is an island, but is rather part of a fabric, and no individual thread in that fabric has a meaning except to the extent that it is part of an organic whole. The idea of existence as being fundamentally relational is far from new; one especially succinct formulation is J. Krishnamurti’s adage “To be is to be related”, but I am sure that those of you who have studied philosophy will be able to cite similar formulations from earlier centuries. One thing that modern mathematics has added to this viewpoint is the idea of isomorphism, and more broadly the category-theory perspective, but that’s a topic for another time. (Though if you’re impatient to learn more about this, check out what Tai-Danae Bradley has written, listed in the References.)

A relational ontology naturally supports a relational epistemology as well. Here’s what mathematician Barry Mazur has to say about what it means to understand mathematical objects like numbers: “Objects are understood by the network of relationships they enjoy with all the other objects of their species.” So to truly understand the number two, we’d have to understand the twin prime conjecture, and the Artin conjecture, and the answers to important questions about the number two from the future of mathematics — questions we don’t even know how to ask yet. But part of what makes math exciting is how much we have yet to learn.

Who knows two? I don’t know two. And I’m okay with that.

Thanks to Tai-Danae Bradley, Sandi Gubin, Brian Hayes, Evelyn Lamb, Andy Latto, Mike Lawler, Colm Mulcahy, Shecky Riemann, Tomas Rokicki, and James Tanton.

Next month: Time and Tesseracts.

ENDNOTES

#0. I still haven’t figured out how to create links that will allow easy navigation between the main text and the Endnotes. If any of you are WordPress gurus, or have seen WordPress sites that get this right, please let me know!

#1. Here I am, like a man of seventy years (only younger); yet until embarrassingly recently I spelled “Pharaoh” as “Pharoah”.

#2. In English, we say “the whole megillah” (from the Hebrew word for a scroll containing the entire Book of Esther) to mean “the whole long story”, but “the whole haggadah” would be more appropriate.

#3. A different problem with Frege’s approach to number is finding the right logical framework to embed it in. Cantorian set theory won’t do, because the class of all sets that have n elements is too big to itself be a set. One fix for this problem is to use some sort of stratified set-theory, the way I just did when I used the word “class” to denote a collective that’s too big to be a set.

#4. Someone who knows five a lot better than I do is John Baez, who’s made a whole hour-long video about it. He also has a  video on the number eight and a video on the number twenty-four.

#5. I’ll assume that you’re already convinced, if you do a faro out-shuffle in a deck with 2n cards, the card that starts at position i ends up in position j where j is the remainder you get when you divide 2i by 2n−1; and I’ll assume that you want to understand next how to leverage this fact to get an understanding of the effects of repeated shuffling. If you out-shuffle a second time, the card that was in position j moves to position k, where k is the remainder you get when you divide 2j by 2n−1. But there’s another way to describe k: it’s the number you get when you divide 4i by 2n−1. Here’s why: Since j is the remainder you get when you divide 2i by 2n−1, j differs from 2i by a multiple of 2n−1. So j − 2i is a multiple of 2n-1. But doubling a multiple of 2n−1 always gives a multiple of 2n−1, so 2(j − 2i) = 2j − 4i is a multiple of 2n−1. This implies that 2j differs from 4i by a multiple of 2n−1, so they leave the same remainder when you divide them by 2n−1.

The same argument shows that if you do three faro out-shuffles, the card that started in position i will end up in the position whose number is the remainder when 8i is divided by 2n−1. And so on.

#6. Since 2⁸−1 is a multiple of 51, it follows that for every i between 1 and 50, 2⁸ i − i = (2⁸ − 1) i is a multiple of 51. But this tells us that 2⁸ i leaves remainder i when we divide it by 51. And that in turn tells us that after 8 out-shuffles, the ith card is back where it started.

#7. Why did Gauss get interested in learning about the order of a mod p as a function of a and p? The value of a he was most interested in was not 2 but 10, because he was studying the problem of determining the length of the repeating part (the “repetend”) in the decimal expansions of fractions. For instance, in the fraction 1/7, with decimal expansion 0.142857142857…, the repetend is 142857, with length 6. Gauss showed that when p is prime, the length of the repetend in the decimal expansion of 1/p is the order of 10 mod p, which is at most p−1. How many primes p are there for which the decimal expansion of 1/p has length p−1? We still don’t know whether the number of such primes p is finite or infinite. It’s equivalent to the problem of determining whether there are infinitely many primes for which 10 is a primitive root. For more on fractions that like 1/7 have interesting decimal expansions, see Gardner’s essay “Cyclic Numbers”.

#8. Let’s start with a method for solving the Riddler problem that doesn’t work, but which will lead us to a method that does: Suppose we look for a three-digit solution abc. What would it take for the decimal value of cab (namely 100c+10a+1b) to be twice the decimal value of abc (namely 100a+10b+1c)? If we expand and simplify the equation 100c+10a+1b = 2(100a+10b+1c), we get 98c = 190a+19b, or (after dividing by 19) 98c/19 = 10a+1b. This can’t work because the right hand side is a whole number, whereas the left hand side can’t be a whole number, because neither 98 nor c is a multiple of 19. (Well, you might think c=0 works, but then we get a=b=0, and 000 isn’t a positive integer.)

This attempt failed because 10²−2 is not a multiple of 19. But, turning this around, what if we found an exponent m such that 10^m−2 was a multiple of 19? Then we’d have a solution. What might such an m be like? Here we can use a slightly indirect approach. If 10^m is 2 more than a multiple of 19, then (multiplying by ten) we see that 10^m+1 is 20 more than a multiple of 19, which is to say, 1 more than a multiple of 19. Meanwhile, Euler’s theorem tells us that 10¹⁸ is 1 more than a multiple of 19. So we might guess that m+1 is 18, that is, that m is 17. Sure enough, it works: (10¹⁷−2)/19 = 5263157894736842. For an explanation of where to go from there, see the official solution. Part of what’s interesting about the problem is that if you try to use Excel or an ordinary calculator to find an m such that 10^m is 2 more than a multiple of 19, you probably won’t succeed; Excel only keeps track of 16 digits, and most calculators keep track of fewer.

#9. My own exposure to Artin’s conjecture came in high school, as a result of my daydreaming during Latin class. In first year Latin we learned how to “decline” nouns and adjectives from tables like this:

To learn the entries in the table, we recited them by columns: “mensa, mensae, mensae, mensam, mensa, mensae, mensarum, mensis, mensas, mensis”. I noticed that if you instead read the entries by rows, the recitation is the same for the first three entries: “mensa, mensae, mensae, mensarum, mensae, mensis, mensam, mensas, mensa, mensis”. In fact, if the declension table looked like

it would read the same by both rows and columns. This got me wondering, what can you say about a two-column table with n rows that reads the same whether you recite its entries by rows or by columns?

I noticed that for certain values of n, tables that are required to read the same both ways are forced to be pretty boring: all of the entries besides the first and last have to be the same. But then I got to thinking that it’s kind of interesting that there are so many values of n that force the table to be boring.

It turns out that those values of n are precisely the ones for which 2n−1 is a prime with the property that 2 is a primitive root modulo 2n−1. And if you think about it, it isn’t so strange that my question about imaginary variants of Latin would be connected to the study of primitive roots, because when you take a two-column table that’s supposed to be read column by column, and instead you read it row by row, what you’re doing amounts to a faro shuffle!

#10. Mathematics offers many other paradoxical situations where we can’t prove that any particular proposition in a list of propositions is true, even though we can show that at least one of them must be. An elementary example is the list of ten propositions “The decimal expansion of pi contains the digit i infinitely often”, as i ranges from 0 to 9. None of these ten propositions has been proved yet, though the irrationality of pi tells us that at least two of them are true, and experimental evidence strongly suggests that all ten of them are. Some logicians contend that such paradoxes teach us that we need to be more careful about the way we handle the word “or”. In intuitionistic mathematics, the proposition “At least one of the ten digits occurs infinitely often in the decimal expansion of pi” is not (yet) a theorem, because the proof hinges on a principle of logic that intuitionists reject: the law of the excluded middle. So, if we’re curious about the way minds know numbers, we’re going to want to look harder at the ways intutionists know numbers! But that’s another telling for another time.

REFERENCES

(If you’re reading hardcopy of this blog essay, keep in mind that most of my References are web-documents, and that the online version of the essay has the relevant links. Also, if you know of any good reference works that I should add, especially web-accessible ones, please let me know! This blog-essay is an evolving document.)

Tai-Danae Bradley, “The Most Obvious Secret in Mathematics”. For those with more advanced mathematical background, there’s a related essay “The Yoneda Perspective”.

Persi Diaconis and Ronald Graham, Magical Mathematics: The Mathematical Ideas  That Animate Great Magic Tricks.

Persi Diaconis, Ronald Graham, and William Kantor, “The Mathematics of Perfect Shuffles”.

Martin Gardner, “Chicago Magic Convention”, in  “The Unexpected Hanging and Other Mathematical Diversions.”

Martin Gardner, “Card Shuffles”, in “Mathematical Carnival”.

Martin Gardner, “Cyclic Numbers”, in “Mathematical Circus”.

Richard Hamming, “The Unreasonable Effectiveness of Mathematics”, 1980.

Barry Mazur, “When is one thing equal to some other thing?”.

Warren McCulloch: “What Is a Number, that a Man May Know It, and a Man, that He May Know a Number?”.

Pieter Moree, “Artin’s primitive root conjecture — a survey”.

M. Ram Murty, “Artin’s conjecture for primitive roots”.

Vickie Neale, “Closing the Gap: The Quest to Understand Prime Numbers”.

Numberphile, “The Best (and Worst) Ways to Shuffle Cards“.

Numberphile, “52-Card Perfect Shuffles”.

Numberphile, “Looking at Perfect Shuffles”.

Jane Shore, “Who Knows One” (published in the April 2, 2018 issue of  the New Yorker, pp. 70-71). https://www.newyorker.com/magazine/2018/04/02/who-knows-one

Paul Stepahin, “Shuffling”. The essay includes a link to a nice animation that demonstrates the shuffling process for a 22-card deck.

Eugene WIgner, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”, 1960.

Wikipedia, “Artin’s conjecture on primitive roots”.