“The fourth dimension became a thing you talked about, without knowing what it meant.”
— Marcel Duchamp
“The fourth dimension!” The mere phrase makes some small part of my brain shiver. And it’s not just me that feels that there’s something awe-full, and maybe awful, about the fourth dimension. 16th-century scholar Gerolamo Cardano1 said it was contrary to Nature. 17th-century thinker John Wallis2 found the very idea of it monstrous. And now 21st century virtual-reality pioneers are about to bring it into your home, if you want it there.
One of the most famous monsters inhabiting the fourth dimension is the tesseract, which you might have heard mentioned ever-so-briefly in the recent film “A Wrinkle in Time”. The movie is based on the classic book by Madeleine L’Engle, which has introduced generations of children to the idea of dimensions beyond the three that we see around us.
WHAT EXACTLY ARE WE TALKING ABOUT HERE?
When I say “the fourth dimension”, I’m not talking about time (though physicists both before and after Einstein have drawn great explanatory power from viewing space and time as part of a single four-dimensional fabric). A crucial thing about the ordinary three dimensions of our world is that they’re directions that you can travel in at will, watching the scenery change as you move outward and then home again. When we travel in time (as we can’t help doing with every heartbeat), we certainly see changes in the scenery, but we can’t make a return trip from the Future to the Present, and that makes time a different sort of dimension than, say, altitude. (And it’s also a bit incoherent to say that one travels from one’s past to one’s future, unless one is also willing to say that one’s anatomy “travels” from one’s head to one’s toes.)
Also, when I say “the fourth dimension”, I’m not talking about the kind of ultra-puny (and still hypothetical) hidden extra dimensions that string theorists posit to account for the embarrassing discrepancy between the three-plus-one dimensions we can see and the eleven dimensions string theory predicts (read practically anything by physicist Brian Greene if any of this eleven-dimensions stuff is news to you). If the universe has extra directions that are rolled up the way the theory requires, then your body can’t travel in those directions; or rather, your body’s constituent particles already are zipping around in those directions, circling the universe the short way round fajillions of times per second.
So what do I mean by the fourth dimension? Before I answer, let’s amend the phrase “the fourth dimension”. Why should dimensions come in some particular order? Our three-dimensional space comes with no preferred direction, and if it doesn’t look that way to you, it’s because you’re distracted by the local scenery. Out between the galaxies, one direction looks much like any other, and you and your intergalactic friends could choose three perpendicular directions to serve as coordinate axes for purposes of facilitating meetups, but there’d be no reason to single out one of the directions as the “first” direction, or the “second”, or the “third”. One of the things that gives space its spacey-wacey-ness is that all the different directions are mixed up. So instead of focussing on a particular dimension as being the “fourth”, we should focus on spaces that have (exactly) four dimensions.
So what do I mean by a four-dimensional space? I mean a space that at every points admits four mutually perpendicular lines, in no particular order, but not five.
Now, a practical-minded person would say that there’s no such thing as this kind of four-dimensional space and impatiently move on. And a mystical-minded person might seize on the idea of The Fourth Dimension as an emblem of wonders that are forever beyond the reach of the human mind. But a mathematical-minded person asks “What might we be able to know about four-dimensional space even if we have trouble imagining it?”
Mathematicians have adopted the axiom that, just as every two-dimensional slice of Euclidean three-dimensional space obeys the laws of two-dimensional Euclidean geometry, every three-dimensional slice of Euclidean(esque) four-dimensional (hyper)space should obey the laws of three-dimensional Euclidean geometry. Once this axiom has been accepted, a host of logical consequences follow readily, even though our imaginations follow slowly, if at all.
Some of these consequences should interest the practical-minded person who impatiently walked away two paragraphs back, since the mathematics of higher-dimensional spaces plays a huge role in the modern world. For instance, Google’s pagerank algorithm is based on multidimensional linear algebra. People can’t visualize million-dimensional spaces (and Google’s servers can’t visualize anything at all), but the mathematics of million-dimensional spaces is part of what makes efficient internet search possible.
SEEING THE UNSEEABLE
Just as the cube serves as the exemplar of three-dimensional space, the tesseract serves as the exemplar of four-dimensional space. The word “tesseract” was coined by mathematician Charles Howard Hinton (from an obscure Greek prefix meaning “four”). It’s more common nowadays to call the tesseract a hypercube, though the term “hypercube” is also used generically to refer to an n-dimensional cubes for any value of n bigger than 3.
The tesseract entered popular culture through Madeleine L’Engle’s “A Wrinkle in Time”, though L’Engle caused some of her readers confusion when one of the characters in “A Wrinkle in Time”, the prodigy Charles Wallace Murray, declared “Well, the fifth dimension’s a tesseract.” L’Engle wasn’t sure how to reconcile Hinton’s ideas about the fourth dimension with Einstein’s, so she put Hinton’s fourth dimension after Einstein’s, demoting it from fourth place to fifth. (Perhaps she should have had Charles Wallace call time the zeroeth dimension!)
One way to depict a tesseract is to drop the constraint that the four dimensions be perpendicular to one another in our depiction. This poses no problems for those of us who’ve grown up with Western ideas of perspective, since we’re used to the idea that lines that are perpendicular in the real world don’t usually look perpendicular in photographs, drawings, or paintings. Here’s one view of a tesseract, very similar to one I showed earlier, but rotated slightly, and with colors added:
 The picture shows a network of struts joining the sixteen corners of a hypercube. Here I’ve drawn the struts in red, blue, green, and orange, according to the four hyperspace directions (depicted with their mutual angles being multiples of 45 degrees, instead of all being 90 degrees as perpendicularity would require). If you ignore the orange edges, you can temporarily convince your brain that the red, blue, and green struts are perpendicular to one another, forming two overlapping red-blue-green cubes. Or, if you ignore the green edges, you can convince your brain that what you’re seeing are two red-blue-orange cubes. What you can’t make your brain do is see the red-blue-green parallelepipeds as being cubes and see the red-blue-orange parallelepipeds as being cubes at the same time — let alone do the same for the other two ways of attending to just three of the four colors.
The picture shows a network of struts joining the sixteen corners of a hypercube. Here I’ve drawn the struts in red, blue, green, and orange, according to the four hyperspace directions (depicted with their mutual angles being multiples of 45 degrees, instead of all being 90 degrees as perpendicularity would require). If you ignore the orange edges, you can temporarily convince your brain that the red, blue, and green struts are perpendicular to one another, forming two overlapping red-blue-green cubes. Or, if you ignore the green edges, you can convince your brain that what you’re seeing are two red-blue-orange cubes. What you can’t make your brain do is see the red-blue-green parallelepipeds as being cubes and see the red-blue-orange parallelepipeds as being cubes at the same time — let alone do the same for the other two ways of attending to just three of the four colors.
The use of two-dimensional pictures as cartoons of the tesseract is reminiscent of the way 20th century artists like Picasso sought, in the Cubist movement, to create two-dimensional images incorporating multiple incompatible perspectives. Obtaining a four-dimensional view is thus a matter combining three-dimensional views that in our world are irreconcilable. If we cease from this struggle and just accept irreconcilability, we switch over to a less ambitious two-dimensional perspective, and then those would-be cubes are seen as perfectly compatible parallelepipeds.
Here’s a very different picture of a hypercube:
 Notice that, as in the earlier colored picture, there are sixteen dots, and each of them is joined to its neighbors by four differently-colored struts. To turn it into a hypercube, you’ll have to make some modifications of this picture, or, as L’Engle might have said, you’ll have to “wrinkle” it. First, print it out (if you’re reading this on a screen) and then cut it out along the dotted lines, obtaining a square. Now join the top edge to the bottom edge, obtaining a cylinder, and then join the left edge (which is now a circle) to the right edge (also a circle). What? You were able to do the first step, but not the second? Sorry, my mistake. Go back to the flat square, join the left edge to the right edge, obtaining a cylinder, and then join the top edge (which is now a circle) to the bottom edge (also a circle). What? You still couldn’t do both steps? Even though you were able to do each of them separately? Oops, I forgot to tell you: to do the joining properly, without distortion, you’d need to use the fourth dimension.
Notice that, as in the earlier colored picture, there are sixteen dots, and each of them is joined to its neighbors by four differently-colored struts. To turn it into a hypercube, you’ll have to make some modifications of this picture, or, as L’Engle might have said, you’ll have to “wrinkle” it. First, print it out (if you’re reading this on a screen) and then cut it out along the dotted lines, obtaining a square. Now join the top edge to the bottom edge, obtaining a cylinder, and then join the left edge (which is now a circle) to the right edge (also a circle). What? You were able to do the first step, but not the second? Sorry, my mistake. Go back to the flat square, join the left edge to the right edge, obtaining a cylinder, and then join the top edge (which is now a circle) to the bottom edge (also a circle). What? You still couldn’t do both steps? Even though you were able to do each of them separately? Oops, I forgot to tell you: to do the joining properly, without distortion, you’d need to use the fourth dimension.
Since we live in a three-dimensional world, you’ll have to tolerate some distortion. Replace the piece of paper by something as stretchy as bubble gum; then you can fold up the square to forum a torus (the surface of a doughnut). The vertices A, B, C and D will form the vertices of a square, and so will the vertices A, E, I, and M.
Another common picture of a tesseract is this one (as interpreted by Ben Orlin):
This looks like a little cube inside a big cube, but we’re invited to conceive of the little cube as being the same size as the big cube — it only looks smaller because it’s farther away from us in the fourth dimension. This picture was very common when I was young, but I always found it confusing, because it seemed wrong to apply perspective principles to the fourth dimension but then not apply them (or only apply them minimally) to the other three. But I think it’s the best picture to use if you want to try to count all the edges (can you find all 32?) and all the faces (can you find all 24?). If you cut away 4 of those faces (the ones that intersect the line running through Ben Orlin’s “handle”), you can see the torus I mentioned a little while ago.
Yet another projection of the hypercube is the rhombic dodecahedron, with its fourteen vertices (six of degree 4 edges and eight of degree 3):
 To get the picture I really have in mind, you’ll need to imagine a fifteenth vertex in the very middle of the solid, joined to the eight vertices of degree 3. This picture should be thought of as a higher-dimensional analogue of the perhaps familiar way of obtaining a regular hexagon as a very symmetrical projection of a cube:
To get the picture I really have in mind, you’ll need to imagine a fifteenth vertex in the very middle of the solid, joined to the eight vertices of degree 3. This picture should be thought of as a higher-dimensional analogue of the perhaps familiar way of obtaining a regular hexagon as a very symmetrical projection of a cube:
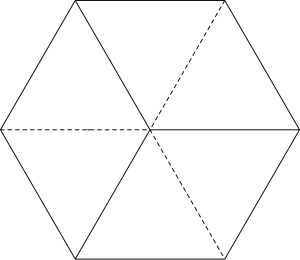 Here I’ve drawn some of the edges as dashed lines, to suggest the edges of the cube that aren’t visible because they’re obscured by other bits of the cube. The middle of the hexagon is simultaneously a projection of the cube’s front vertex and back vertex. In the same way, the extra vertex that we added in the middle of the rhombic dodecahedron is simultaneously the projection of the hypercube’s front vertex and back vertex, in the fourth dimension. The four not-really-perpendicular axes here are the four diagonals of a cube, which are mutually at 60 degree angles.
Here I’ve drawn some of the edges as dashed lines, to suggest the edges of the cube that aren’t visible because they’re obscured by other bits of the cube. The middle of the hexagon is simultaneously a projection of the cube’s front vertex and back vertex. In the same way, the extra vertex that we added in the middle of the rhombic dodecahedron is simultaneously the projection of the hypercube’s front vertex and back vertex, in the fourth dimension. The four not-really-perpendicular axes here are the four diagonals of a cube, which are mutually at 60 degree angles.
The rhombic dodecahedron offered us an orthographic projection of a hypercube (parallel lines stay parallel), and the little-cube-in-a-big-cube picture offered us a central projection (some parallel lines appear to meet). Yet another way of projecting four-dimensional space into three-dimensional space is stereographic projection. With this sort of projection, the edges of the hypercube become circular arcs. Later on I’ll show you the wonderful use that mathematician and artist Henry Segerman makes of this style of projection.
I’ll mention one final and rather brutal way to bring the tesseract down to human scale: break it open and squash it. When we do this with the surface of a cube, we reduce it to a cross in two dimensions, made of six squares:
 If we do something similar with a hypercube, we reduce it to a solid in three dimensions, made of eight cubes:
If we do something similar with a hypercube, we reduce it to a solid in three dimensions, made of eight cubes:
Dali incorporated this “octocube” into his painting “Crucifixion (Corpus Hypercubus)”. Dali’s painting combines modern mathematical ideas of the fourth dimension with the transcendent ideas expressed by the philosopher Henry More, who in his metaphysicial text Enchiridion Metaphysicum (1671) wrote: “Besides the three dimensions which are filled with all extended material things, a fourth must be admitted, with which coincides the spirit.”
HEARING THE UNSEEABLE
An entirely different modality we can use in trying to apprehend higher dimensions is music. Classical music offers many examples of “cubes” — musical passages that, when plotted in two dimensions (with time as the horizontal axis and pitch as the vertical axis), look like the plane projection of the vertices of a parallelipiped. A very nice one comes from the 8th, 9th, 10th, …, 14th, and 15th notes of J. S. Bach’s Fugue in B minor, from the Well-Tempered Clavier (I am indebted to Scott Kim for bringing this example to my attention). I single this one out because as it happens there’s a YouTube video that highlights the geometrical aspect of this musical cube:
Noam Elkies has pointed out some examples of musical hypercubes, but none of them are as auditorially salient as the Bach example. One of the examples Elkies noticed is a passage in the middle movement (Scherzo: Allegretto vivace) of Beethoven’s Piano Sonata Opus 31 #3:
 If we ignore sharps and flats, those thirty-two notes can be seen as a plane projection of a five-dimensional “parallelotope”. Elkies has shown me other examples of four- and five-dimensional cubes in classical music, and fugues are especially abundant sources, but in most instances the time-delay between themes and repetitions obscures the geometric structure of the passage. Also, many of the examples involve some fudging with the sharps and flats.
If we ignore sharps and flats, those thirty-two notes can be seen as a plane projection of a five-dimensional “parallelotope”. Elkies has shown me other examples of four- and five-dimensional cubes in classical music, and fugues are especially abundant sources, but in most instances the time-delay between themes and repetitions obscures the geometric structure of the passage. Also, many of the examples involve some fudging with the sharps and flats.
Can any readers point me toward other examples of hypercubes, perhaps in 20th century music? The whole project of serial music seems like it would be well-suited to such experiments.
FUN AND GAMES
One way to get a feeling for an abstract mathematical structure is to play with it. As a teenager, I convinced many of my friends to play four-dimensional tic-tac-toe, which I learned about from a Martin Gardner column, reprinted in “Hexaflexagons and Other Mathematical Diversions”.
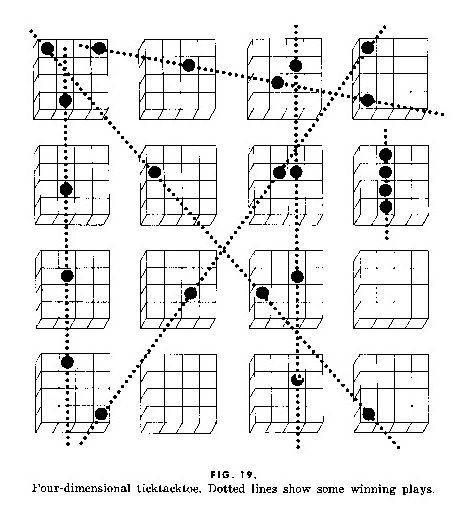
From “Ticktacktoe” (chapter 4 in “Hexaflexagons and Other Mathematical Diversions” by Martin Gardner); permission pending.
Nowadays I suspect many children have their first four-dimensional experience playing Marsha Falco’s game Set, whose 81 cards can be viewed as the points in a 3-by-3-by-3-by-3 grid whose four “dimensions” are color, number, shading, and shape.
Sometimes a puzzle has a hidden four-dimensional aspect. The famous Tower of Hanoi puzzle, with n disks on three pegs, turns out to be equivalent to the problem of constructing a Hamiltonian path on an n-dimensional hypercube. (See chapter 6, “The Icosian Game and the Tower of Hanoi”, in “Hexaflexagons and Other Mathematical Diversions”.) So if you’ve ever solved the 4-disk version of the Tower of Hanoi, you’ve been effectively traveling on the surface of a tesseract, whether or not you were thinking about it that way.
Another puzzle that has a hidden four-dimensional aspect is one that Martin Gardner learned about from Scott Kim (which I in turn learned about from reading Gardner): Can you place sixteen knights on a chessboard so that each of them attacks exactly four others? See Endnote 4 for the solution.
BRINGING TIME INTO THE PICTURE
In some ways, it’s silly to try to learn about the fourth dimension from two-dimensional still images or even from three-dimensional static objects. After all, the way we learn about our three-dimensional world is by seeing how its appearance changes when we move through it. So it’s natural to use time as a tool for understanding the behavior of a (spatial) fourth dimension.
Mathematician Tom Banchoff has been a pioneer of using computer animation to make the fourth dimension accessible, and his classic video “The Hypercube: Projections and Slicing” is worth watching.
Another video you might enjoy is “Understanding 4D — The Tesseract”:
It’s natural to model the sixteen vertices of the hypercube as the sixteen points (a,b,c,d), where I’m using quadruples to represent points in the usual “Cartesian coordinates” way (but with four dimensions instead of just two or three), and where each of the numbers a, b, c, d is either 0 or 1. This is the point of view lurking beneath the surface of Federico Ardila’s video, listed in the References. A different model uses the coordinates −1 and +1 instead of 0 and 1. Then the sixteen points all lie on the hypersphere given by the equation w2+x2+y2+z2=4, and instead of joining them up by line segments, we can join them up by circular arcs that lie on the hypersphere. If we then take these 16 points and 32 arcs and stereographically project them from the hypersphere to ordinary three-dimensional space, we get a tesseract with curved edges. This more organic-looking kind of tesseract is the basis of Henry Segerman’s hypercube zoetrope, which wittily marries 19th century proto-cinematic technology with 21st century object-fabrication technology. You can see it featured in the video Brilliant Geometry: a physical 3D zoetrope of a 4D cube (starting about 9 minutes and 30 seconds in).
STEPPING THROUGH THE PICTURE FRAME
But passive viewing of a dynamically changing image, however rich that image might be, is still only a crude imitation of the way babies achieve fluent understanding of the geometry of the physical world, and convert the “blooming, buzzing confusion” of sense-data into a three-dimensional mental map. Would a baby with its hands and legs bound (warning: don’t try this at home!), watching the world through the gaps in its crib, ever learn to make sense of space? Of course not! And yet, when it comes to the fourth dimension, we’re that baby. Or we were, until computer-generated reality came into the story. We can now learn about the 4D world by moving through it and interacting with it.
For instance, check out Jeff Weeks’ 4-d games (4D Maze, 4D Draw) that you can play with on your smartphone.
One way to get a feeling for high-dimensional objects in four dimensions and beyond is to take a “walk” around them and survey them from multiple angles. If this interests you, you might want to play with Ggobi (pronounced “gee-gobi”), a statistical visualization package that includes as one of its methods the ability to take a “grand tour” of a high-dimensional object. Visit http://www.ggobi.org/ (the grand tour is is described in section 5.4 of the manual).
Tom Banchoff told me about the work of Marc ten Bosch (http://marctenbosch.com/). I’d already played with Marc’s 4D Toys app on my smartphone, but I never got a good feeling for it. (The blurb calls 4D Toys “a box of toys from the fourth dimension. It turns out the rules of how objects bounce, slide, fall, spin and roll around can be generalized to any number of dimensions, and this toy lets you experience what that would look like.” There’s a short video about it.) Marc’s other project, Miegakure, a platform game that integrates exploring the fourth dimension with solving puzzles, was totally unknown to me. You can get a feel for the game by watching the video “Designing a 4D World: The Technology behind Miegakure”. If any of you have experience with the game, please post a comment!
Henry Segerman told me about a game called “hypernom” that he and others have developed, best played on an iOS or Android device, available at http://hypernom.com. By rotating your device around, you can move through a tiling of the three-sphere, eating the cells of your choice of 4D polytope. More details are at http://elevr.com/hypernom/.
An especially promising avenue for those who want to get a kinesthetic understanding of the fourth dimension is virtual reality. Albert Hwang discusses his own efforts to understand hypercubes in his video “What does VR reveal about the 4th dimension?”
With the advent of virtual reality, a long-deferred part of Hinton’s dream can finally be realized. In thinking about how one might come to understand the fourth dimension, Hinton realized that children might have more luck than their parents, since the youthful brain is more malleable; he also realized that in some ways humans don’t get to develop three-dimensional intuition the way birds and fish do, since unlike creatures of the air and the sea, we mostly move in two dimensions. He therefore made a point of creating climbing structures for his young children, and devising games that could be played on those structures, with the goal of enhancing the children’s appreciation of three dimensions. One of those children, Sebastian Hinton, went on to develop the idea and patented what today we call the “jungle gym”.
Nowadays we view climbing jungle gyms as just a form of physical recreation, but Hinton would have seen it as a way of learning about three-dimensional space, and a prologue to a new chapter in the awakening of the human species to consciousness of higher dimensions. He would have loved the sort of ropy and foamy geometrical structures kids get to climb on nowadays, and probably would have invented games for kids to play on those structures, as a prod toward internalizing three-dimensional geometry. But still, those are three-dimensional structures. Now, thanks to virtual reality, we can give our children experiences conducive to internalizing four-dimensional geometry. It will be interesting to see what happens next.
Thanks to Tom Banchoff, Edwin Clark, Noam Elkies, David Feldman, Sandi Gubin, George Hart, Scott Kim, Evelyn Lamb, Mike Lawler, Jeannine Mosely, Gerry Myerson, and Henry Segerman.
Next month: Why does “Exploding Dots” work?
ENDNOTES
#1. Cardano, in his Ars Magna (1545), wrote (describing the powers of numbers), “For as the first power refers to a line, the square to a surface, and the cube to a solid body, it would be fatuous indeed for us to progress beyond, for the reason that it is contrary to nature.”
#2. John Wallis, in his book Algebra (1685), wrote: “Nature, in propriety of Speech, doth not admit of more than Three (Local) Dimensions. A Line drawn into a Line shall make a Plane or Surface; this drawn into a Line, shall make a Solid: But if this Solid be drawn into a Line, or this Plane into a Plane, what shall it make? A Plano-plane? That is a Monster in Nature, and less possible than a Chimaera or Centaur. For Length, Breadth and Thickness, take up the whole of Space. Nor can our Fancy imagine how there should be a Fourth Local Dimension beyond these Three.”
#3. It’s interesting to zoom in on the transaction that occurs when, by accepting an axiom about four-dimensional spaces, the mind gets a kind of theoretical purchase on concepts that cannot be directly imagined with any kind of vividness. As Bertrand Russell wrote (in his review of Hinton’s book “The Fourth Dimension”): “[I]f such purely intellectual constructions as the fourth dimension are to be permissible, it is surely necessary to emancipate our logic from the degrading dependence on perceptible space to which Kant condemned it.” And yet, the relationship between physical experience on the one hand, and the mathematical idea of a fourth dimension on the other hand, is a subtle one. Certainly the existence of a fourth dimension is contradicted by experience in our every waking moment. And yet, the idea of the possibility of a fourth dimension is obtained by combining physical experience with the non-physical idea of extrapolation and analogy. Would any philosophers reading this essay care to comment on whether Russell is being fair to Kant in this passage?
#4. Place the knights at points corresponding to the vertices of a hypercube:
REFERENCES
Edwin A. Abbott, Flatland: A Romance of Many Dimensions, 1884.
Federico Ardila, “Combinatorics and higher dimensions” (video). This video inspired Mike Lawler to make a video about showing Ardila’s video to his kids.
John Baez, “Symmetry and the Fourth Dimension”. For purposes of this essay, you might want to start with Part 11 and Part 12.
Thomas Banchoff, “History of Thought: Four-Dimensional Geometry”.
Davide Cervone, “Beyond the Third Dimension” (virtual exhibition available in Portuguese and English).
Davide Cervone, “Some Notes on the Fourth Dimension” (a collection of materials Cervone put together for a course on the fourth dimension described in the Union College newsletter).
David Darling and Agnijo Banerjee, “Weird Math” (see chapter 2, “How to See in 4-D”).
Martin Gardner, Hexaflexagons and Other Mathematical Diversions. See chapter 4 (“Ticktacktoe”) and chapter 6 (“The Icosian Game and the Tower of Hanoi”).
Martin Gardner ,Mathematical Carnival. See chapter 4 (“Hypercubes”).
Charles Howard Hinton, The Fourth Dimension, 1904. (Does anyone know whether he is related to the writer S. E. Hinton? Denizens of the fourth dimension would certainly deserve the moniker “The Outsiders”.)
Kelsey Houston-Edwards, Dissecting Hypercubes with Pascal’s Triangle (video, PBS Infinite Series). This video inspired Mike Lawler to make a video about showing Houston-Edwards’ video to his kids.
Mike Lawler, HyperCubeB (video). This walk-around of a model of Bathsheba Grossman’s version of the tesseract is downright spooky; it sure looks like the thing is changing, even though the only thing that’s changing is our perspective! Mike and his kids made two videos about this: one in October of 2016 and the other a couple of weeks later.
Madeleine L’Engle, A Wrinkle in Time, 1962.
Matt Parker, Things to Make and Do in the Fourth Dimension.
Matt Parker, Four Dimensional Maths: Things to See and Hear in the Fourth Dimension (video).
Rudy Rucker, Geometry, Relativity and the Fourth Dimension.
Bertrand Russell’s review of Hinton’s book The Fourth Dimension.
Hannah Fry and Thomas Rutherford, “The Fifth Dimension” (podcast).
Jody Trout, “History of the Fourth Dimension” (PowerPoint presentation).





I must be missing the point of the square you can join left to right, or top to bottom, but not both. You don’t have to go to the 4th dimension to make both joins – you just have to make the whole thing out of rubber instead of paper, and you get a donut, in three dimensions. Does that help me visualize the tesseract?
LikeLiked by 1 person
Pingback: Who Knows Two? |
I don’t think you are missing the point at all; I was just being too narrow. (Sometime I’ll edit the paragraph to say something like “For the price of some geometric distortion, we can replace paper by rubber, and then the sixteen points become …”) Notice that the four-colored octagonal depiction of the hypercube can be seen as a transparent polyhedral torus, as can the little-cube-in-a-big-cube picture.
LikeLike
The unfolded hypercube makes its appearance in an amusing short story of Heinlein’s (“And He Built a Crooked House”), about an overly enthusiastic Southern California architect who builds a house on that design (inverted, if I remember right), which then folds up on itself during an earthquake, with the new owners stuck inside. (You surely know of it, since it’s collected in a book by Clifton Fadiman that includes two mathematical short stories by Martin Gardner as well. “The No-sided Professor” is a classic.)
LikeLike
Pingback: Pieces of April « Log24
Pingback: My talk at the 2018 Williams College math camp | Mike's Math Page
This isn’t well known, but the rhombic dodecahedron isn’t just a visual shadow of the tesseract – the rhombic dodecahedral figurate numbers are formed from the first differences of the fourth dimensional tesseract numbers. Rhombic dodecahedral numbers can count the number of points on the surface of a tesseract etc..
The tesseract numbers are:
[1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000]
Take the first differences via n^4 – (n – 1)^4 and you get:
[1, 15, 65, 175, 369, 671, 1105, 1695, 2465, 3439, 4641]
https://oeis.org/A005917

See the png for a visualisation. afaik there is no published work exploring this fact.
LikeLiked by 1 person
That’s a neat fact. And I like the cannonball arrangement for the rhombic dodecahedron; not something I’d seen before!
LikeLike
Professor,
I hope you don’t mind me posting this here (I can’t think where else).
I noticed it was possible to further connect the rhombic dodecahedral figurate numbers to the differences of the fourth powers:
[14, 50, 110, 194, 302, 434, 590, 770, 974..] are the second differences of the fourth powers and they count the number of points in the outer shell of the RD figurate number.
[36, 60, 84, 108, 132, 156, 180, 204..] are the third differences. I wasn’t able to find an exact match, but this sequence +2 counts the number of points in an outer net of a RD.

Shown here:
Since the nth differences of the nth powers = n factorial, the next set of differences = 4!.
I noticed it was possible to reproduce this in some way with the cubes. That is, the second to last differences of the cubes count a figurate outer net which increases by 3!

Shown here:
This made me wonder – since the third from last differences of the nth powers are always a cubic sequence, are there any matching 3D figurate numbers for higher powers? If so, could they have any connection to the factorial?
Apologies for going OT.
LikeLike
Pingback: Who Knows Two? - My Blog